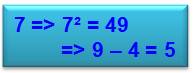Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 31/12/2023 M'écrire Brèves de Maths

INDEX Carrés Puissances Énigmes virales Jeux et énigmes	Carrés
	Carrés	Introduction	Formes	Fraction = carré
	Unités	Derniers chiffres	Terminaison	Chiffres des carrés
	Progression	Triplets de Pythagore	Différences carrés	Second degré
	Écarts	Quadruplets diophantiens

Faites un double-clic pour un retour en haut de page

Chiffres des carrés Différence et, occasion d'une énigme Prendre les chiffres du carré et les soustraire. Montrer seulement ce résultat et faire deviner l'opération. Exploration sur ce thème: opération avec les chiffres du nombre, les chiffres du carré et les chiffres du cube.
	Sommaire de cette page >>> Énigme du 4567 qui donne 5335 >>> Somme-Différence des chiffres du carré >>> Somme-Différence des chiffres du nombre >>> Somme-Différence des chiffes du cube	Débutants Nombres géométriques Glossaire Nombres géométriques

Énigme du 4567 qui donne 5335		haut
Énigme Avec ces trois premières relations, dont la partie intermédiaire est à découvrir, reconstituer la quatrième. Remarque Vous trouverez cette énigme sur le Net avec cette présentation que je continue à dénoncer car elle usurpe la signification du signe égal et elle peut conduire à entretenir une confusion dans l'esprit des jeunes.	Données de l'énigme
Piste Le titre de la page vous met sur la voie … Oui, il faut calculer le carré des nombres. Alors, 4 devient 4² = 16. Reste un pas facile à franchir pour imaginer que 5 est la différence entre 6 et 1, les chiffres du carré. Solution Notez Voyez comment avec ce procédé 4567 devient 5335, un nombre palindrome.

Voir Brève 56-1115

Somme-Différence des chiffres du carré		haut
Méthode Calcul du carré. Différence entre le chiffre des unités et celui des dizaines, et cela jusqu'à 9² = 81. Pour 10 et plus, cette différence est ajoutée à la différence entre centaines et milliers.	Exemples 2 => 2² = 4 => 4 7 => 7² = 49 => 9 – 4 = 5 9 => 9² = 81 => 1 – 8 = – 7 12 => 12² = 144 => (4 – 4) + (1 – 0) = 1 32 => 32² = 1024 => (4 – 2) + (0 – 1) = 1 99 => 99² = 9801 => (1 – 0) + (8 – 9) = 0
Différence des chiffres des carrés des nombres jusqu'à 99 Record pour la somme en valeur absolue pour n jusqu'à un million Le tableau montre les valeurs jusqu'au carré de un million. La liste continue et, sans doute, la somme-différence progresse jusqu'à l'infini. Ex: 1500303^3 = 2250909091809 => 48 2022827^3 = 4091829071929 => 49

Somme-Différence des chiffres du nombre		haut
Méthode Cette fois, on utilise les chiffres du nombre et on applique le même procédé. Ex: 609 => (9 – 0) + (6 – 0) = 15 Pour un million, la somme record n'est jamais négative et elle stagne à 27. Cependant, il suffit d'ajouter à gauche un couple des mêmes chiffres pour obtenir un nouveau record. Ex : 9090909 => 4 × 9 = 36	Record pour la somme des chiffres du nombre en valeur absolue pour n jusqu'à un million

Somme-Différence des chiffes du cube		haut
Méthode Même procédé appliqué aux chiffres du cube. Ex: 9^3 = 729 => (9 – 2) + (7 – 0) = 14 Le tableau montre les valeurs jusqu'au cube de un million. La liste continue et, sans doute, la somme-différence progresse jusqu'à l'infini. Ex: 1634112^3 = 4363605270708092928 => 57 1826259^3 = 6090979075939091979 => 62 …	Record pour la somme des chiffres du cube en valeur absolue pour n jusqu'à un million

Haut de page (ou double-clic)

Suite	Terminaison des carrés Les nombres carrés Système décimal – Unités Terminaisons des produits Cycle des chiffres des carrés Puissance 1001 Divisibilité de différence de puissances d'un nombre Puissances terminées par 00…01 Nombres et les chiffres de leurs puissances Unités des produits
Voir	Carrés – Calcul mental Carrés – Somme pour nombres successifs Carrés somme de cubes Chemin d'Euler Chiffres dans leurs puissances Cubes – Calcul mental Cubes – Modulo Cubes – Somme pour nombres successifs Dualité Énigme virales sur le Net Exponentielle Nombres automorphiques Nombres géométriques Partition & Addition Permutation des chiffres et puissances Racine carrée Racines - Calcul
Cette page	http://villemin.gerard.free.fr/aNombre/MOTIF/Chiffres/ChifCarr.htm