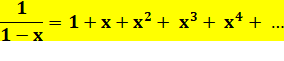NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 03/10/2024 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Maths en se divertissant
Débutants Général	BRÈVES de MATHS									Glossaire Général
INDEX Brèves Atlas des maths	Page 1	Page 10		Page 20		Page 30		Page 40			Page 50
	Page 20 (380-399)		Page 21 (400-419)		Page 22 (420-439)		Page 23 (440-459)		Page 24 (460-479)
	Page 25 (480-499)		Page 26 (500-519)		Page 27 (520-539)		Page 28 (540-559)		Page 29 (560-579)

BRÈVES de MATHS – Page 25

Un millier de faits et chiffres

sur les nombres et les mathématiques

Ces pages sont dédiées à tous ceux qui veulent aborder les mathématiques en douceur et en s'amusant tout en découvrant les aspects les plus fondamentaux de cette discipline. Un parcours à picorer avec nombreux liens d'orientation vers les développements destinés à satisfaire votre curiosité.

En principe ces pages sont très abordables sans connaissances particulières de maths. Elles sont proposées dans un ordre quelconque favorisant la découverte de sujets multiples.

Anglais: Facts and figures about numbers and mathematics

480. Quadrature du triangle
But Transformer le triangle quelconque en un carré de même taille avec une construction à la règle et au compas. Construction Triangle quelconque ABC et la hauteur issue de C et son milieu D. Perpendiculaire en B à AB. Cercle de centre B et de rayon CD. Intersection avec AB en E. Milieu F de AE pour tracer le cercle vert. Intersection G. BG est le côté du carré.		GB² = BA.BE = BA.CD Aire du carré = Aire du triangle
Brèves associées	>>> Triangle du pitre à bord		>>> Types de triangles
Pour en savoir plus	>>> Quadrature du triangle		>>> Quadrature du cercle

481. Carré magique 3x3 et permutations
Le but est de repartir les nombres de 1 à 9 dans une grille 3x3 de sorte que les sommes sur les lignes, les colonnes et les diagonales soient égales. La somme magique sera 15. Il existe 9! = 362 880 façons de disposer ces nombres, mais seules huit répondent aux conditions indiquées. Même! Une seule est la mère des sept autres, obtenues par permutations des emplacements. La figure montre ces carrés en visualisant la position du 1 et du 2 pour mettre en évidence les permutations.
Brèves associées	>>> Carré magique 6x6 – Construction		>>> Carrés magiques – Index
Pour en savoir plus	>>> Le carré magique 3x3 – Sa programmation >>> Permutations		>>> Nombre 362 880

482. Paradoxe de Banach-Tarski
Paradoxe devenu théorème Il est possible de couper une boule en un nombre fini de morceaux et de réassembler ces morceaux pour former deux boules identiques à la première, à un déplacement près. Démontré en 1924 par Stefen Banach et Alfred Tarski.		Récréer deux sphères identiques à partir d'une seule est évidemment infaisable en pratique. Ce théorème fait appel à des notions situées aux confins des mathématiques avancées: Axiome de choix, Dénombrable et continu, Infini façon "hôtel de Hilbert" Théorie de la mesure
Brèves associées	>>> Nœuds, entrelacs et tresses		>>> Paradoxe de la corde à l'Équateur
Pour en savoir plus	>>> Sphère		>>> Sphères magiques

483. Premier au carré
Un nombre premier au carré, sauf 2 et 5, est un multiple de 24 plus 1. La démonstration se base sur le fait qu'un nombre premier est toujours un voisin d'un multiple de 6. On porte au carré et on montre que ce carré est divisible par 12 et par 2.
Brèves associées	>>> Premiers en 6k+1 et 6k+5		>>> Premiers en brèves – Index
Pour en savoir plus	>>> Premier au carré		>>> Nombre premier >>> Nombre carré

484. Nombres NRC – Nombre x Retourné = Carré

Nombres carrés, produits d'un nombre et de son retourné.

Exclus les nombres en 0 tels que 200 x 2 = 400 = 20²

Exclus les nombres palindromes tels que 101 x 101 = 101²

Table avec le nombre, son retourné, le produit et sa racine carrée

144	×	441	=	63504	=	252²
169	×	961	=	162409	=	403²
288	×	882	=	254016	=	504²
441	×	144	=	63504	=	252²
528	×	825	=	435600	=	660²
768	×	867	=	665856	=	816²
825	×	528	=	435600	=	660²
867	×	768	=	665856	=	816²
882	×	288	=	254016	=	504²
961	×	169	=	162409	=	403²
1089	×	9801	=	10673289	=	3267²
1584	×	4851	=	7683984	=	2772²
2178	×	8712	=	18974736	=	4356²
4851	×	1584	=	7683984	=	2772²
8712	×	2178	=	18974736	=	4356²
9801	×	1089	=	10673289	=	3267²
10404	×	40401	=	420332004	=	20502²
10609	×	90601	=	961186009	=	31003²
10989	×	98901	=	1086823089	=	32967²
12544	×	44521	=	558471424	=	23632²
12769	×	96721	=	1235030449	=	35143²
13104	×	40131	=	525876624	=	22932²
14544	×	44541	=	647804304	=	25452²
14884	×	48841	=	726949444	=	26962²
15984	×	48951	=	782432784	=	27972²
20808	×	80802	=	1681328016	=	41004²

Brèves associées

>>> Retournés proportionnels

>>> Brèves Sur formes et motifs – Index

Pour en savoir plus

>>> Nombres retournés

>>> Nombres carrés

485. Palindromes ou Retournés
Palindrome: nombres qui se lisent aussi bien de gauche à droite (normal) que de droite à gauche comme: 123321. Palindromes premiers Il y a 90 palindromes de 1000 à 9999 comme: 1001, 1111, 1221, 1331, 1441, 1551, 1661, 1771, 1881, 1991, 2002, 2112, 2222, 2332, 2442, 2552, 2662, … Aucun n'est premier; ils sont tous divisibles par 11. En effet, un nombre est divisible par 11 si la somme des chiffres de rang pair et égale à celle de rang impair. Pour 1551 on a bien: 1 + 5 = 5 + 1		Nombre et son retourné: le nombre et lui-même, lu à l'envers, comme 1234 et 4321. Nombres et retournés premiers Comme 1009 et 9001 qui sont premiers tous les deux. Ils sont 204 couples de premiers sur les 9000 à quatre chiffres, comme: 1009, 1021, 1031, 1033, 1061, 1069, 1091, 1097, 1103, 1109, 1151, 1153, 1181, 1193, 1201, 1213, 1217, 1223, 1229, …
Ne pas confondre les deux notions: palindrome et retourné !
Brèves associées	>>> Nombres palintiples		>>> Type de nombres en brèves – Index
Pour en savoir plus	>>> Palindromes >>> Retournés		>>> Divisibilité par 11

486. Série 1/ (1 – x)
		Exemple x = 0,5 1 + 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 = 127 / 64 = 1,98… 1 + 1/2 + … + 1/10^10 = 1,9990 … 1 + 1/2 + … + 1/10^20 = 1,9999990 …
Brèves associées	>>> Suite de Sherlock Holmes		>>> Brèves sur les suites – Index
Pour en savoir plus	>>> Séries en 1 / (1 – x)		>>> Suites et séries >>> Série harmonique

487. Partitions et Pentagonaux
Partitions d'un nombre entier n Ce sont toutes les additions possibles ayant n pour somme. Une des partitions de 5 est 3 + 2. Nombres pentagonaux (généralisés) Ce sont les nombres de la forme G = 1/2 n(3n 1) Les premiers de la liste: 0, 1, 2, 5, 7, 12, 15, 22, 26, 35, 40, …			Théorème des nombres pentagonaux Découverte merveilleuse de Leonhard Euler (1717-1783). Ce théorème permet le calcul de la quantité de partitions en se référant aux nombres pentagonaux de la manière indiquée ci-dessous.
Calcul des quantités de partitions par récurrence Les indices en rouge sont les nombres pentagonaux. Le signe alterne de deux en deux.
Brèves associées	>>> Partitions et décompositions			>>> Maths en Brèves – Index
Pour en savoir plus	>>> Théorème des nombres pentagonaux >>> Nombres pentagonaux			>>> Euler

488. Diagramme de Ferrers
Manière de présenter toutes les partitions d'un nombre sous forme géométrique. Ici, les sept partitions du nombre 5. Ce mode de représentation joue un rôle important pour dénombrer les partitions. Par exemple, trouver les partitions strictes, celles avec seulement des nombres distincts. Ici: 5, 4 + 1 et 3 + 2 (les trois sous la diagonale). Ces partitions strictes comptent une quantité paire ou impaire de lignes. Il se trouve que ces deux quantités sont égales pour tous les nombres qui ne sont pas pentagonaux généralisés. Voir Chapitre Partitions, juste ci-dessus.
Brèves associées	>>> Partitions strictes		>>> Maths Numération – Index
Pour en savoir plus	>>> Diagramme de Ferrers		>>> Nombre 8 avec diagramme de Ferrers

489. Nombres polygonaux
Les nombres polygonaux jouent à la courte échelle: pour passer d'un nombre pentagonal d'ordre k à celui d'ordre k + 1, il suffit de lui ajouter le nombre triangulaire d'ordre k. Exemple Soit le nombre triangulaire 15 pour n = 5. Pour n = 6, le triangulaire est 15 + 6 = 21. Et pour calculer le carré, on ajoute 15 et 21 = 36. Pour calculer le pentagonal, on ajoute 15 et 36 = 51. Etc.		Nombres polygonaux Sur chaque colonne du tableau, on progresse du nombre de tête de la colonne précédente (le triangulaire précédent).
Brèves associées	>>> Carrés et hexagonaux		>>> Nombres en Brèves – Index
Pour en savoir plus	>>> Différence entre polygonaux		>>> Nombres polygonaux – Table

490. Nombres triangulaires – Formule

Sachant que la suite des nombres triangulaires est: 1, 3, 6, 10, 15, 21

Quelle est la formule définissant chacun ?

Les écarts sont en progression arithmétique. Il s'agit d'une fonction quadratique; cad. du deuxième degré en ax² + bx + c.

Écrivons trois relations avec les nombres connus et résolvons ce système de trois équations à trois inconnues.

Résolution du système d'équations

(1)	1²a	+ 1b	+ c	= 1
(2)	2²a	+ 2b	+ c	= 3
(3)	3²a	+ 3b	+ c	= 6
(4)=(2)-(1)	3a	+ b		= 2
(5)=(3)-(2)	5a	+ b		= 3
(6)=(5)-(4)	2a			= 1
	a			= 1/2
		b		= 1/2
			c	= 0

Bilan

Brèves associées

>>> Nombres triangulaires

>>> Brèves de maths – Index

Pour en savoir plus

>>> Nombres triangulaires

>>> Système d'équations

491. Puissance de 2 et divisibilité par 3
La somme de deux puissances de 2 consécutives est divisible par 3. Une puissance de 2 accolée (concaténée) à la suivante forme un nombre divisible par 3.		Exemples 2^5 = 32 et 2^6 = 64. La somme 96 est divisible par 3. Le nombre 3264 est divisible par 3. Vrai aussi en permutant: 6432 est divisible par 3.
Brèves associées	>>> Divisibilité par 8		>>> Brève sur les divisibilités – Index
Pour en savoir plus	>>> Divisibilité par 3		>>> Puissances de 2

492. Divisibilité par 3 – Induction
Propriété: Tout nombre en n^3 + 2n est divisible par 3. Démonstration par induction 1) Propriété vraie pour n = 1: 1^3 + 2x3 = 3, divisible par 3. 2) Hypothèse: vraie pour n: n^3 + 2n est divisible par 3 (on dit que c'est vrai ! À voir ?).		3) Calcul pour n = k + 1: (k + 1)^3 + 2 (k + 1) = k^3 + 3k^2 + 3k + 1 + 2k + 2 = (k^3 + 2k) + 3(k² + k + 1) Or, selon l'hypothèse (k^3 + 2k) est divisible par 3. Le second terme, avec le facteur 3, est divisible par 3. Donc, toute l'expression est divisible par 3. 4) Propriété vraie pour 0 et vraie pour n+1, lorsque vraie pour n, alors par induction, vraie tout le temps ∎
Brèves associées	>>> Divisibilité de A^n – B^n		>>> Brève sur les divisibilités – Index
Pour en savoir plus	>>> Divisibilité par 3		>>> Démonstrations par induction

493. Année 2016 – Minimale
2016 = 720 + 1296		Cette propriété permet de résoudre le défi de la somme minimale pour les années autour de 2016. Par exemple, il suffit des quatre premiers chiffres, dans l'ordre, pour arriver à 2016. On remplace 6 par 3!, car factorielle 3 = 1 x 2 x 3.
Brèves associées	>>> Année 2018 et ses chiffres		>>> Brèves Jeux – Index
Pour en savoir plus	>>> Nombre 2016 >>> Année 2016		>>> Jeu de la somme minimale >>> Factorielle

494. Puissances de consécutifs
Sommes de consécutifs 1 + 2 + 3 + 4 = 10 2 + 3 + 4 + 5 + 6 = 20 4 + 5 + 6 + 7 + 8 = 30 6 + 7 + 8 + 9 = 30		Mêmes sommes avec la puissance qui suit (1 + 2 + 3 + 4)^5 = 100 000 (2 + 3 + 4 + 5 + 6)^7 = 1 280 000 000 (4 + 5 + 6 + 7 + 8)^9 = 19 683 000 000 000 (6 + 7 + 8 + 9)^10 = 590 490 000 000 000
Brèves associées	>>> Nombres pannuériques		>>> Brèves Motifs – Index
Pour en savoir plus	>>> Puissances avec des consécutifs		>>> Puissances

495. Multiplications avec les doigts
Ce sont les tables de multiplications après 5 qui sont les plus difficiles à retenir. Voici un vieux truc utilisant les doigts. Procédé 1. Numérotez les doigts de 6 à 10. 2. Pour multiplier 7 par 8, faites toucher les doigts 7 et 8. 3. La quantité de doigts en bas donne les dizaines. 4. Le produit des doigts en haut donne les unités.
Brèves associées	>>> Multiplication par 9 – Avec les doigts		>>> Brèves Calculs – Index
Pour en savoir plus	>>> Multiplications avec les doigts		>>> Tables de multiplication

496. Centre de gravité du quadrilatère
Le point M, intersection des médianes (bleues), est le centre géométrique du quadrilatère. C'est le centre de gravité des quatre sommets (cad. le centre de gravité d'un objet vide avec une masse identique située sur chacun des sommets). Le point G est le centre de gravité du quadrilatère (objet matériel de masse homogène répartie sur toute la surface). Sa localisation n'est pas simple (Voir le lien: en savoir plus). En règle générale, les points M et G sont distincts.
Brèves associées	>>> Carré divisé – Aire manquante		>>> Brèves géométrie – Index
Pour en savoir plus	>>> Quadrilatère et ses "milieux"		>>> Centre de gravité

497. Battre les cartes
Mélanger les cartes 6 fois suffit pour disposer des cartes réparties aléatoirement. Le mélange américain (riffle shuffle) est le plus efficace: couper le paquet en deux et regrouper les deux paquets en intercalant leurs cartes respectives. Il y a une transition abrupte entre 6 et 8 mélanges: moins de 6 et c'est mal mélangé, plus de 8 et c'est parfait. Ce phénomène a été mis en évidence dans de nombreux processus aléatoires. L'état d’équilibre est atteint non pas progressivement, mais de manière abrupte. Avec une mélange par coupes successives à la française, il faudrait 10 000 opérations pour atteindre la perfection. En prenant la carte du dessus et en l'insérant n'importe où dans le paquet, 205 opérations (en moyenne: n log n) sont nécessaires.
Brèves associées	>>> Énigme du parking	>>> Brèves Jeux – Index
Pour en savoir plus	>>> Cartes et hasard	>>> Réussite aux cartes

498. Théorème de Ptolémée
Théorème Pour un quadrilatère inscrit, le produit des diagonales est égal à la somme des produits des côtés opposés: Cas du rectangle Avec a = c, b = d et m = n, alors: Le théorème de Pythagore est un cas particulier du théorème de Ptolémée. Pythagore (-580 à -495) Ptolémée (v.100 à v168)
Brèves associées	>>> Th. de Pythagore – Visuel >>> Ptolémée et nombre d'or		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Théorème de Ptolémée		>>> Ce théorème en trigonométrie

499. Factorielles et carrés
Produit de trois factorielles consécutives. 4! x 5! x 6! = 2 073 600 = 1 440² Le tableau montre la construction du carré final. En jaune un carré naturel et en rose un carré plus inattendu: 2 x 3 x 4 x 6 = 6! / 5 = 720 / 5 = 144 = 12²
Brèves associées	>>> Pépites numériques		>>> Brèves Motifs – Index
Pour en savoir plus	>>> Factorielles et carrés		>>> Carrés >>> Factorielles

Retour	Brèves de maths – Page 24
Suite	Brèves de maths – Page 26
Voir	Voir liens en haut de page
Cette page	http://villemin.gerard.free.fr/NombDico/aBreves/Breve25.htm