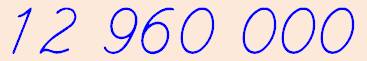Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 26/03/2020 M'écrire Brèves de Maths

DicoNombre Débutant Glossaire Types de nombres Nom des nombres Écriture des nombres Table des facteurs Langues	Dictionnaire des Nombres
	0 / 0,… / 1 / 10 / 100 / 200 / 300 / 400 / 500 / 600 / 700/ 800 / 900 / 1 000 / 2 000 / 5 000 / 10 000 / 100 000
	10^6	10^7	10^8	10^9	10^10	10^20	10^50	10^100	10^1000	Infini
			1296m	5 10^7

Douze-millions-neuf-cent-mille.

Twelve million, nine hundred sixty thousand.

Facteurs
Notation	1,296 × 10^7
Puissances	= 60^4 = (3 x 4 x 5)^4 = 3 600^2
Diviseurs	Quantité: 225
Binaire	1100 0101 1100 0001 0000 00002
Bases	441000012 C5C10016 10 00060

Suite

Composé

Abondant

Puissant

12 960 00010 = 10 00060 = 1x60^4 + 0x60^3 + …	Vaut dix mille en sexagésimal.
12 960 000 = 3 600² = 36² x 100² = 2 700 x 4 800	Nombre de Platon.
12 960 000 = 3 749 x 3 456 + 3 456 = 1 000 x 12 959 + 1 000	Repdigit en base 3 749. La plus petite. Exemple repdigit pour la base 1000.
12 960 000 / (1 + 2 + 9 + 6) = 720 000 12 960 000 / 225 = 57 600	Harshad Nombre Tau
12 960 000 = 7 + 12 959 993 = …	Somme de nombres premiers.
12 960 000 = 1 008² + 3 456² = 2 160² + 2880²	Deux fois somme de deux carrés. Notez le terme en 3456.

Connu des Babyloniens pour sa grande quantité de possibilités de divisions. Malgré cette grande quantité de diviseurs, ce nombre est loin d'être hautement composé: 720 720 en a 240 – plus que 225; 14 414 400 en a 512 – nombre proche avec plus de deux fois plus de diviseurs.

Géométrie

12 960 000 Quantité de secondes d'arc dans DIX cercles. 10 x 360 degrés x 60 minutes x 60 secondes

>>>

Identité détaillée

Diviseurs, {1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 16, 18, 20, 24, 25, 27, 30, 32, 36, 40, 45, 48, 50, 54, 60, 64, 72, 75, 80, 81, 90, 96, 100, 108, 120, 125, 128, 135, 144, 150, 160, 162, 180, 192, 200, 216, 225, 240, 250, 256, 270, 288, 300, 320, 324, 360, 375, 384, 400, 405, 432, 450, 480, 500, 540, 576, 600, 625, 640, 648, 675, 720, 750, 768, 800, 810, 864, 900, 960, 1000, 1080, 1125, 1152, 1200, 1250, 1280, 1296, 1350, 1440, 1500, 1600, 1620, 1728, 1800, 1875, 1920, 2000, 2025, 2160, 2250, 2304, 2400, 2500, 2592, 2700, 2880, 3000, 3200, 3240, 3375, 3456, 3600, 3750, 3840, 4000, 4050, 4320, 4500, 4800, 5000, 5184, 5400, 5625, 5760, 6000, 6400, 6480, 6750, 6912, 7200, 7500, 8000, 8100, 8640, 9000, 9600, 10000, 10125, 10368, 10800, 11250, 11520, 12000, 12960, 13500, 14400, 15000, 16000, 16200, 16875, 17280, 18000, 19200, 20000, 20250, 20736, 21600, 22500, 24000, 25920, 27000, 28800, 30000, 32000, 32400, 33750, 34560, 36000, 40000, 40500, 43200, 45000, 48000, 50625, 51840, 54000, 57600, 60000, 64800, 67500, 72000, 80000, 81000, 86400, 90000, 96000, 101250, 103680, 108000, 120000, 129600, 135000, 144000, 160000, 162000, 172800, 180000, 202500, 216000, 240000, 259200, 270000, 288000, 324000, 360000, 405000, 432000, 480000, 518400, 540000, 648000, 720000, 810000, 864000, 1080000, 1296000, 1440000, 1620000, 2160000, 2592000, 3240000, 4320000, 6480000, 12960000}

Voir Diviseurs, Quantité, Somme, Fonctions arithmétiques

Nombre de Platon – Nombre nuptial Nombre géométrique de Platon		haut
La République de Platon – Livre VIII Texte philosophique ésotérique dans le quel Platon commence par un casse-tête dont il n'a pas donné la solution. Platon annonce: Il existe, pour ce qui est d'origine divine, une période dont rend compte un nombre parfait (sens de particulier de parfait différent de celui d'aujourd'hui). Le nombre nuptial régit les bons et les mauvais mariages. Il correspondrait à une période entre les générations. (The lord of better and worse births). Platon déclare que la durée idéale de la vie humaine est de 100 ans soit 100 x 360 = 36 000 jours. Le nombre nuptial correspond à 360 fois cette valeur: 36 000 x 360 = 12 960 000.	Texte traduit (extraits) C'est le nombre primordial dans lequel les multiplications dominatrices et dominées … arrivent à produire avec tous ces facteurs un système cohérent de parties aliquotes. Leur base sesquitierce accouplée avec cinq, quant à elle augmentée trois fois, produit deux harmonies l'une exprimée par un carré dont le côté est multiple de cent, l'autre par un rectangle construit d'une part sur cent carrés des diagonales rationnelles de cinq, diminués chacun d'une unité, ou des diagonales irrationnelles, diminués de deux unités, et, d'autre part, sur cent cubes de trois..
Platon a utilisé explicitement le nombre 729 = 9^3 pour donner une "distance" entre le bonheur du tyran et celui du roi. En revanche, le nombre 12 360 000 est plus mystérieux. Ce serait le nombre qui contiendrait la "loi des justes accouplements".	Interprétation courante Utilisation des nombres du triplet isiaque: 3, 4, 5, considérés comme principes de l'univers. Son produit: 3 x 4 x 5 = 60 Platon dit: trois fois augmenté, soit trois puissances par rapport à la puissance 1, soit 4: Le nombre devient: 60^4 = 12 960 000 Certains ont une autre interprétation Le triplet: 3, 4, 5 Trois fois augmenté, soit chacun au cube. Ce qui donne: 3^3 + 4^3 + 5^3 = 216.
Le triplet de base	La base sesquitierce (3, 4) est accouplée à 5. Sesquitierce est effectivement un nombre accompagné de lui-même plus son tiers: 3 et 3 + 1/3 x 3 = 4
Deux harmonies Interprétation	12 960 000 = (3 x 4 x 5)^4 = 36² x 100² (harmonie 1 – carré) = 4 800 x 2 700 (harmonie 2 – rectangle)
Calcul des dimensions du rectangle Platon arrive à nous faire faire ce calcul de surface d'un rectangle	100(7 x 7 – 1) = 100 x 48 = 4 800 pour un côté 100 x 3^3 = 100 x 27 = 2 700 pour l'autre côté
Cas de 48 et son calcul Qui est exprimé curieusement. Rejoignant le nombre de Platon avant sa multiplication par 10 000.	48 x 27 = 36 x 36 = 6^4 = 1 296
Harmonie	Terme issu d'une interprétation à partir des intervalles entre notes de musique.
Origine babylonienne Utilisation de la base 60 Pour eux le nombre 60^4 = 12 960 00010 = 10 00060 Les textes Babyloniens mentionnent de nombreuses fractions avec ce nombre pour numérateur.	Ce nombre aurait été utilisé par cette civilisation notamment pour désigner un nombre élevé, mais indéterminé. Platon connaissait très bien ce dix mille des Babyloniens.
Autres propositions pour le nombre de Platon Outre 12 960 000 et 216	17 500 = 100 x 100 + 4 800 + 2 700 760 000 = 750 000 + 10 000 = 19 x 4 x 10000 8 128 = 2^6 (2^7 – 1) 1 728 = 12^3 = 8 x 12 x 18 5 040 = 144 x 35 = (3 + 4 + 5)^2 (2^3 + 3^3)

Anglais Plato's nuptial number / Allemand die Platonische Zahl

Explications largement inspirées de la référence Marc Denkinger

Elle s'applique à la manipulation des nombres et non sur l'exégèse du texte

L'explication de Philippe Remacle

Le fond épitrite (sesquitierce) de ces éléments...	3 et 4.
accouplé au quinaire...	multiplié par 5; ce qui donne le produit : 3x4x5.
trois fois multiplié par lui-même...	élevé à la quatrième puissance.
fournit deux harmonies...	deux expressions:
l'une égale un nombre égal de fois, autant de fois cent...	1) formée par un carré dont le côté est multiple par cent: (3x4x5)^4 = 12 960 000 = (36x100)^2.
l'autre équilatérale en un sens, mais rectangle...	2) la figure est dite équilatérale parce que ses côtés sont égaux deux à deux.
construite d'une part sur cent carrés des diamètres rationnels de cinq...	le diamètre rationnel de cinq est le nombre rationnel le plus proche de racine de 50, diagonale d'un carré ayant 5 pour côté. Ce nombre est 7, et son carré 49.
diminués chacun de l'unité...	49 – 1 = 48.
ou des diamètres irrationnels diminués de deux...	Le diamètre irrationnel de 5 est racine carrée de 50. Son carré diminué de deux unités est égal à 48. Les Muses indiquent deux moyens de trouver ce nombre, qui doit être multiplié par 100.
et, d'autre part, sur cent cubes de trois.	Soit 2 700. La seconde harmonie, exprimée par le rectangle : 4 800 x 2 700 = 12 960 000 = (3x4x5)^4, est donc bien formée, elle aussi, par le produit, élevé à la quatrième puissance, des éléments 3, 4 et 5 du triangle cosmique.

Largement inspiré du texte de Philippe Remache – Livre VIII

Suite	Voir Haut de page / Autres nombres
Voir	Nombres par leur nom Empreinte des nombres DicoNombre Junior Historique de ce site et Références Maitres en nombres
Sites	Nombre de Platon – Wikipédia L'énigme du Nombre de Platon et la Loi des dispositifs de M. Diès – Marc Denkinger – 1955 L'Antiquité grecque et latine du moyen âge – Philippe Renacle et als Platon – La République – Livre VIII – (543a – 568c) – Philippe Remacle et als The Republic of Plato – James Adam – 1902 (réédité en 2010)
Cette page	https://diconombre.pagesperso-orange.fr/N10P6/N10P7/N12960m.htm