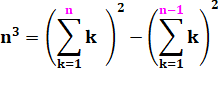Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 22/02/2025 M'écrire Brèves de Maths

DicoNombre Débutant Glossaire Types de nombres Nom des nombres Écriture des nombres Table des facteurs Langues	Dictionnaire des Nombres
	0 / 1 / 10 / 100 / 200 / 300 / 400			500 à 599			600 / 700 / 800 / 900 / 1 000 / 2 000 / 5 000 / 10 000 / 100 000 / 10^6 / 10^9 / 10^100
	500	510	520	530	540		550	560	570	580	590
	510	511	512	513	514	515		516	517	518	519

Cinq-cent-douze.

Five hundred twelve.

Orthographe / Langues

Facteurs	= 8^3
Binaire	10 0000 0000 1 000 000 000
Octal Hexa	1000 200
Bases	2002223 200004 13317 24215 [16, 16]31 8863 44127 22255
Romain	DXII

Suite

ABA

Auto-nombre

Composé

Constructible

Cube doublement cube

Déficient (de 1 seulement)

Dudeney

Friable (3-friable)

Frugal

Harshad

Harshad à Q-carré

Leyland

Pratique

Puissance de 2

Woodall

Architecture

512 m La tour Burj de Dubaï mesure 512 mètres. Record de hauteur de construction en 2007.

>>>

Nombres de Dudeney

Nombres de Dudeney: nombres narcissiques qui sont égaux au cube de la somme de leurs chiffres. Ils sont cinq:

512 = 8³ ; 4 913 = 17³ ; 5 832 = 18³ ; 17 576 = 26³ ; 19 683 = 27³.

Chiffres et numération

512 => 5 et 1, 2	Plus petite puissances de 2 ayant plus de chiffres impairs que de chiffres pairs. La suivante est 2^17.
512 + 215 = 727	Devient palindrome en lui ajoutant son retourné.

Addition et soustraction

512	Aucune somme de nombres consécutifs (rare) >>>
512 = 8^3 = 57 + 59 + … + 71	Somme d'impairs consécutifs.

Multiplication, division, diviseurs

512 = 2!^9

Produit (trivial) de factorielles.

5 + 12 = 17 51 + 2 = 57

Nombres premiers formés avec un signe plus entre les chiffres.

512 = (5 + 1 + 2) x 64 = (5 + 1 + 2)^3	Nombre de Harshad avec chiffres distincts: divisible la somme de ses chiffres, cette somme au carré et cette somme au cube. Nombre digipuissant ou nombre de Dudeney Nombre égal au cube de la somme de ses chiffres: suivants: 4 913, 5 832, 17 576 et 19 683.
3^2n+5 + 160n² – 56n – 243		512 divise ce polynôme. Note: En notation moderne, la barre verticale veut dire divise. Voir Démonstration

Deuxième plus petit nombre pour lequel le cumul des sommes de diviseurs est un multiple de 100. Voir Nombre 403

Avec les puissances

512 = 2^9 = 8^3 = 4^4 + 4^4 = 2^8 + 2^8 = 2^4 + 2^4 + 2^4 + 2^4	Nombre frugal Nombre pratique. Puissance de deux. Nombre de Leyland (11^e). Forme: n = x^y +y^x. Mêmes chiffres: 125 = 5^3 et 512 = 2^9 Le nombre et son retourné sont puissants.
512 = 2^9 125 = 5^3 25 = 5^2	Puissances avec les chiffres de 512.
512 = 16² + 16² = 2 x 16² = 4^4 + 4^4	Seule somme de deux carrés >>> Nombre ABA (a.b^a). Nombre ABBA (a^b.b^a) dit de Leyland.
512 = (1 + 2 + …+ 8)² – (1 + 2 + … + 7)² = 36² – 28² = 8^3	Propriété
		Carré + puissance = puissance.
512 = 36² – 28² = (28 + 8)² – 28²		Motif général pour les cubes.
= 36^2 – 28^2 = 4^3 x 2^3		Différence de carré = produit de cubes.
= (5 + 1 + 2) ^3		Curiosité avec les chiffres.
= 8^3 et 5 + 1 + 2 = 8 = 2^3		Nombre de Dudeney. Cube doublement cube. Mêmes chiffres que pour 5^3 = 125.
= 13^2 + 7^3 = 169 + 343		Somme de 2 puissances.

512 = (2 + i 6)^6 = (2 – i 6)^6 –512 = (6 + i2)^6 = (6 – i2)^6 –512 = ( 1 + i3)^9 = ( 1 – i3)^9	Entier = puissance de nombre complexe.
512 = (1 + i)^16 + (1 – i)^16 = (1 + i)^17 + (1 – i)^17	Complexe et puissance de 2.

Dénombrement, jeux et curiosités

Nombre binomial

512 = 2⁸ + 2⁸ = 4⁴ + 4⁴ = 16² + 16²

= 24² – 8² = 36² – 28² = 66² – 62² = 129² – 127²

Autour du nombre

512 x 2^512 – 1 est premier

Nombre de Woodall (13^e).

Décimales

512,73 = 666 – 153,27	Mêmes chiffres après soustraction du nombre de la Bête.
	Selon la classification décimale de Dewey de laquelle fut déduite la classification décimale universelle.
Numérologie Martin Gardner (The Numerology of Dr. Matrix) remarque que la théorie des nombres est codée sous le numéro 512,81 formé avec 2^9 et 9^2. Effet de numérologie qui a conduit à la recoder en 512,73 qui codait les nombres transcendants. Mais, pas de chance: le nombre et une de ses permutations s'arrangent pour donner le nombre maléfique 666. De plus, 153 est le nombre de poissons pêchés par Pierre. David Wells dans son livre (Le Dictionnaire Penguin des nombres curieux – 1995) imagine une suite ésotérique fondée sur le nombre 3. Exemple: 1+5+3= 9 = 3x3 et 3^3 = 27 dont 2+7 = 9. Etc.

Identité détaillée

Voir Diviseurs, Quantité, Somme, Fonctions arithmétiques

Suite	Voir Haut de page / Autres nombres
Voir	Nombres par leur nom Empreinte des nombres DicoNombre Junior Historique de ce site et Références Maitres en nombres
Cette page	http://villemin.gerard.free.fr/NombDico/N5001000/aaaN500/N512.htm