|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
BRÈVES de MATHS – Page 11 Un millier de faits et chiffres sur les nombres et les
mathématiques
En principe ces pages sont très abordables sans
connaissances particulières de maths. Elles sont proposées dans un ordre
quelconque favorisant la découverte de sujets multiples. |
Anglais: Facts and figures about numbers and mathematics
200. Équations diophantiennes |
|
||||
|
Diophante
d’Alexandrie cherchait à résoudre des équations à plusieurs inconnues entières. Voir les développements sur le théorème de
Bézout. |
Exemples 25x + 18y = 1 a pour solution : x = –5 + 18h
et y = 7 + 25k 17x + 5y = 4 a pour solution : x = 1 + 5h
et y = –3 + 17k 28x + 48y = 1 n’a pas de solution car 28 et 48 ne
sont pas premiers entres eux. |
||||
|
Avec
un degré supérieur |
x² + xy + y² =
19 a 12 solutions comme x = 2 et y = 3 x² + y² = z² a une
infinité de solutions (triplets de Pythagore). x² + y² = p a au
moins une solution pour p = 4k + 1. x² + y² + z² +
t² = n a au moins une solution pour tout n. x3 +
y3 = z3 n’a aucune solution. |
||||
|
Brèves liées |
>>> Théorème de Bézout – B161 >>> Triplets de Pythagore – B25 |
||||
|
Pour en savoir plus |
>>>
Équations >>>
Équations diophantiennes |
>>>
Nombres entiers >>>
Diophante (vers 250 de notre ère) |
|||
201. Divisibilité par 5 et modulo |
|
|||
|
Démontrer
que si n est à égal 0 ou 5 mod 10 |
|
|||
|
On se
souvient que, par exemple: C'est une manière d'écrire la division euclidienne en ignorant le
quotient (ici 7). |
73 = 10 x 7 + 3 73 = 10 x k + 3 |
|||
|
n égal 0
mod 10 est un raccourci pour dire => n égal 5
mod 10 est un raccourci pour dire => |
n = 10k = 5 x
2k n = 10k + 5 = 5
(2k + 1) |
|||
|
Que l'on
soit dans le premier cas ou le second: |
n est divisible par 5 |
|||
|
Finalement
notre énoncé savant voulait tout simplement dire qu'un
nombre est divisible par 5 s'il est terminé par 0 ou par 5. |
||||
|
Brèves associées |
>>>
Arithmétique |
|||
|
Pour en savoir plus |
>>>
Arithmétique modulaire (mod) >>>
Exemples d'applications |
>>>
Divisibilité par 5 >>>
Division euclidienne |
||
202.
Toutes les combinaisons = 2k
|
|
|||
|
Exemple avec quatre éléments: A, B, C et D On cherche combien de combinaisons on peut former
si on peut prendre 0, 1, 2, 3 ou 4 éléments à la fois, sans ordre.
Total: 1 + 4 + 6 + 4 + 1 = 16 = 24 Coefficients Vous avez sans doute reconnu la quatrième ligne
du triangle de Pascal. Ces
coefficients sont calculés en utilisant cette formule, par exemple pour 2
parmi 4:
|
Cas général avec k éléments La
généralisation de 4 éléments à k éléments est possible. Si bien que: La somme des combinaisons à partir de k éléments
est égale à 2k. Démonstration express La formule générale du
développement du binôme est la suivante:
Avec
a = b = 1
|
|||
|
Brèves liées |
>>>
Triangle de Pascal |
|||
|
Pour en savoir plus |
>>>
Somme des combinaisons |
>>>
Coefficients du binôme |
||
203.
Nombre de Fermat
|
|
|||
|
Fermat a inventé une race de nombres en puissance
de 2 plus 1 dont les premiers exemplaires sont des nombres premiers. Exemple: 28 + 1
= 257 avec 8 = 23. Effectivement l'exposant
est lui-même une puissance 2. Nombres de Fermat Ils sont donc de la forme:
Les plus petits: 3, 5, 17, 257, 65537 et ces cinq
nombre de Fermat sont premiers Curiosités À partir de 17, ils se terminent tous par 7. Un nombre de Fermat plus 1 est divisible par 6. |
Historique En
1640, Fermat croit avoir découvert une race de nombres dont tous seraient
premiers. Il en fait part à Mersenne et à Pascal. En
1732, Euler trouve que le cinquième nombre de Fermat est composé: F5 = 4 294 967 297 = 641 x 6 700417 Depuis, on n'a pas trouvé d'autres nombres
premiers de Fermat que les cinq plus petits. Amateurs de nombres … Avec
les ordinateurs, la chasse aux nombre de Fermat est ouverte:
|
|||
|
Brèves liées |
>>>
Nombres de Mersenne |
|||
|
Pour en savoir plus |
>>>
Nombres de Fermat >>>
Nombres premiers |
>>>
Puissances de 2 >>>
Fermat (1607-1665) |
||
204.
Isaac
Newton (1642-1727) – 85 ans
|
|
|||
|
Biographie Isaac
Newton: philosophe, mathématicien physicien et astronome anglais. Très
intelligent, Newton commence les études supérieures en 1661 (18 ans) au
Trinity College de Cambridge. En
1665, il s'exile chez sa mère durant un an et demi car l'épidémie de Peste
décime la population de Londres. Durant ce séjour, lui vient l'idée qu'il y a
une relation entre la chute d'un corps sur la Terre et le mouvement de la
Lune (légende de la chute de la pomme). En
1669, il devient titulaire de la chaire de Lucas (comme Stephen Hawking le
sera en 1979). En
1671, il construit le télescope, une invention qui porte son nom. Son
importance reconnue lui vaut d'intégrer la Royal Society. Après
la publication de son livre (1687), il devient célèbre. Il est le président
de la Royal Society. Il est anobli et
devient sir Isaac Newton. Les trois lois de Newton 1) Principe d’inertie Tout corps reste dans l’état
de repos ou de mouvement uniforme en ligne droite dans lequel il se trouve, à
moins qu'une force le contraigne à changer d’état. 2) Principe fondamental de la dynamique Les changements sont
proportionnels à la force motrice, et dans la direction de la force. 3) Actions réciproques L’action est toujours égale
à la réaction. |
Contributions de Newton En
1687, il publie "Principes mathématiques de la philosophie
naturelle". Il
réalise une synthèse à la fois des lois de Kepler sur les orbites planétaires
et de Galilée sur la chute des corps. Il
y expose le principe d'inertie, l'égalité de l'action et de la réaction, les
lois du choc, la proportionnalité des forces et des Mais
surtout, il y parle de sa théorie de l'attraction universelle: les corps
s'attirent avec une force proportionnelle au produit de leur masse et
inversement proportionnelle au carré de la distance qui les sépare. En
1704, il rédige Opticks où il explique que la lumière est en fait constituée
d'un spectre de plusieurs couleurs. Il y traite de la réfraction. Une des
plus grande œuvre scientifique de l'histoire La première loi en amusements Un
enfant reste au repos jusqu'à ce vous lui retiriez la tablette Tout
homme au repos restera au repos, sauf si sa femme le remarque et lui trouve
un boulot à faire. Au
lieu d'une pomme, si Newton avait glissé sur une peau de banane, les lois du
monde auraient été différentes. |
|||
|
Brèves associées |
>>>
Galilée |
|||
|
Pour en savoir plus |
>>>
Newton – Biographie >>>
Newton – Lois >>>
Réfraction |
>>>
Kepler >>>
Humour |
||
205.
Nombre 11 – ONZE
|
|
|||
|
Propriétés Le
nombre 11 est premier. Le plus petit nombre uniforme ou repunit. Multiplication par 11 En
partant de la droite ajouter chaque chiffre avec celui de gauche et recomposer
le nombre en tenant compte des retenues.
Curiosités 11 = 6 + 5 = 6² – 5² 1 / 11 = 0,09 09 09 … Jeux de mots Pie XI était un pape fatigué. Onze la coule douce Onze fait chier |
Curiosités avec les mêmes chiffres
Divisibilité par 11 On
fait la somme des chiffres de rang impair et celle de rang pair. Une égalité indique
que le nombre est divisible par 11.
Un
nombre palindrome ayant une quantité paire de chiffre est divisible par 11.
Les
puissances de 11 sont des nombres palindromes et surtout, ce sont les lignes
du triangle de Pascal. |
|||
|
Brèves associées |
>>>
Nombre 10 >>>
Triangle de Pascal |
>>>
Nombre 12 |
||
|
Pour en savoir plus |
>>>
Nombre 11 – Culture >>>
Nombre 11 – Maths >>>
Multiplication par 11 |
>>>
Divisibilité par 11 >>>
Repunits >>>
Palindromes |
||
206.
Cercle dans le losange
|
|
|||
|
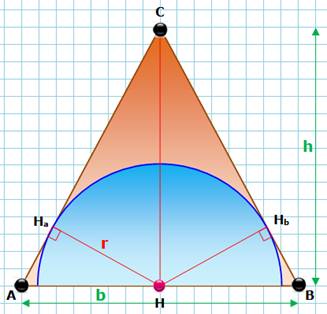
Problème Un triangle isocèle dont la base mesure 16 et la hauteur 15.
Un demi-cercle inscrit comme indiqué sur la figure. Quel est le rayon de ce demi-cercle? Note: cette figure dupliquée vers le bas (symétrie
par rapport à AB) forme un losange avec son cercle inscrit. Remarques Le théorème de Pythagore dans le triangle
rectangle ACH indique:
= 8² + 15² = 64 + 225 = 289 |
|
|||
|
Calcul n°1 Deux évaluations de l'aire du triangle rectangle
ACH
|
Calcul n°2 Deux évaluations du sinus de l'angle en A
|
|||
|
Brèves associées |
>>>
Triangle rectangle |
>>>
Trigonométrie |
||
|
Pour en savoir plus |
>>>
Demi-cercle dans le triangle isocèle >>>
Triangle isocèle >>> Cercle inscrit |
>>>
Théorème de Pythagore >>>
Sinus |
||
207.
Billard d'Alhazen
|
|
|||
|
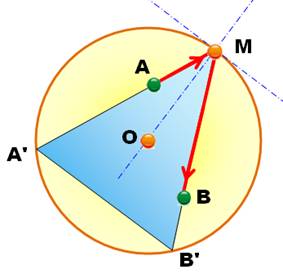
Problème Trouvez
un triangle isocèle inscrit dans un cercle et passant par les deux points
donnés A et B. Déterminez le point M. Solution Il faut résoudre une équation du quatrième degré.
La solution est non constructible avec règle et
compas car elle nécessite l'extraction d'une racine cubique. Historique Problème formulé par Ptolémée en 150. Alhazen, vers l'an 1000, trouve une solution
géométrique à base de coniques. Vers 1500, Leonard de Vinci invente un système
articulé. La solution algébrique est trouvée par Peter
Neumann en 1997. |
Triangle isocèle inscrit passant
par A et B
Problème équivalent Un billard circulaire et deux billes A et B
placées en deux points quelconques. La bille A doit rebondir une fois et
atteindre la boule B. Où se trouve le point de rebond? |
|||
|
Brèves associées |
>>>
Triangle isocèle |
>>> Brève précédente |
||
|
Pour en savoir plus |
>>>
Problème du billard d'Alhazen >>>
Équation du quatrième degré |
>>>
Coniques >>>
Constructible >>>
Racine cubique |
||
208.
Nombre 2 018
|
|
|||
|
Écriture Français: Deux-mille-dix-huit Anglais: Two thousand eighteen Allemand: Zweitausend und achtzehn Identité 2 018 = 2 x 1009 Diviseurs: 1, 2, 1 009, 2 018; somme: 3 030 Nombre déficient (3 030 – 2 018 = 1 012 < 2
018 2018 = 220 220 2 en base 3 (ternaire) Somme de nombres consécutifs 2 018 = 503 + 504 + 505 + 506 Somme de carrés consécutifs 2 018 = 7² + 8² + 9² + …17² + 18² |
Somme de deux carrés 2 018 = 2 x 1009 = 2 x (4 x 252 + 1) Nombre qui n'a pas de diviseur en 4k + 3 (ou qui
a un tel facteur à la puissance 0) => il est somme de deux carrés. Nombre qui n'a qu'un seul facteur en 4k + 1 =>
sa somme en deux carrés est unique.
Somme de puissances 4
Seule possibilité. Remarquez que le 4 manquant au
centre est en puissance. |
|||
|
Brèves associées |
>>>
Nombre 2 017 |
>>>
Nombre 10 >>>
Nombre 100 |
||
|
Pour en savoir plus |
>>>
Nombre 2018 >>>
Nombres en lettres (orthographe) |
>>>
Théorème des deux carrés |
||
209.
Nombres premiers et cryptographie
|
|
||||
|
Problème C'est le problème dit de la factorisation en nombres premiers. Indice pour le quizz: n'oubliez pas le
test de divisibilité par 9 ! |
Exemples
3, 7 et 37 sont des nombres premiers Quizz Sauriez-vous trouver un des facteurs de ce
nombre: n = 123 456 789 ? |
||||
|
La
factorisation n'et pas toujours aussi simple, surtout si les nombres
deviennent grands. À partir d'une certaine taille, il est impossible
de trouver les facteurs, même avec tous les ordinateurs les plus puissants. Cette impossibilité est le point de base de
l'algorithme de cryptographie RSA utilisé pour les transactions bancaires ou
pour assurer la confidentialité sur certains réseaux sociaux. |
Exemples
Ces nombres de 7 chiffres et de 11 chiffres sont
le produit unique de deux nombres premiers. Trouver a et b sans calculette est un peu difficile,
mais faisable. C'est immédiat avec un ordinateur. Exemple avec Maple
|
||||
|
Le code
RSA utilise au moins 2 048 bits, ce qui correspond à 617 chiffres (log10 de 22048)
Facebook ou Gmail utilisent la cryptographie ECC
qui n'est pas basée sur la factorisation. |
Record de factorisation - 155 chiffres en 2009 par Benjamin Moody: 73
jours de calculs. - 232 chiffres la même année: deux ans de
calculs. Le plus grand nombre factorisé à ce jour (2017). Solution du quizz 123 456 789 = 9 x 3 803 x 3 607 Oui, il est divisible par 9. |
||||
|
Brèves associées |
>>> Nombres
2, 3, 5, 7, 11 … Premiers |
>>> Algorithme
de recherche |
|
||
|
Pour en savoir plus |
>>>
Cryptographie RSA >>>
Nombres premiers |
>>>
Divisibilité par 9 |
|
||
210.
Nombre 153 & Cycle-Cube
|
|
|||
|
Procédé itératif du cycle-cube Prenons le nombre 3. Son cube: 33 =
27. La somme des cubes des chiffres: 351. Encore, la somme des cubes: 153. Le nombre 153 marque la fin du procédé. Propriété des multiples de 3 Avec tous les multiples de 3, le procédé finit toujours par 153. La
longueur du cycle est la seule particularité (L = 3 pour le nombre n = 3). Records (n / L) (3 / 3), (6, 10), (117, 11), (177, 13), (12 558,
14). Le cycle ne dépasse par L = 14 itérations
avec n = 12 558, et cela jusqu'à trois millions. |
Cycle-cube pour le nombre 3
Avec le nombre 6, il faut 10
itérations pour finir sur le nombre 153: [216, 225,
141, 66, 432, 99, 1458, 702, 351, 153] |
|||
|
Brèves associées |
>>>
Nombre 153 et la pêche >>>
Procédé de Kaprekar |
>>>
Nombre 100 |
||
|
Pour en savoir plus |
>>>
Cycle –cube >>>
Nombres narcissique |
>>>
Nombre 153 |
||
211.
TABLEUR –
Outils de calcul
|
|
|||
|
Accès au tableur de votre ordinateur Taper
Excel dans la fenêtre en bas à gauche de l'écran.
Ou
alors, cliquez la fenêtre à quatre carreaux et chercher Excel parmi les
programmes listés.
Tapez simplement l'opération précédée du signe = dans la cellule
désirée. Appuyez sur Entrée et le résultat s'affiche dans la cellule. En cliquant sur la cellule, la mémoire de l'opération est affichée
dans la fenêtre d'édition, à côté du fx.
Vous pouvez corriger l'opération dans cette fenêtre. Opération à partir de données existantes
Mise à jour des calculs Désormais,
si vous remplacez 10 ou le 12 par une autre valeur, le calcul est mis à jour
automatiquement. |
Constitution d'une table d'addition Formation de la ligne du haut
Tirez cette poignée jusqu'à 10. (clic gauche enfoncé en déplaçant
cette poignée avec la souris. Les nombres suivants sont placés
automatiquement
Même opération: après saisie du 1 et du 2, tirez la poignée vers le
bas. Addition relative
En ajoutant le symbole $ nous indiquons
que la ligne 1 est fixe, de même que la colonne A. Mettre le symbole * au lieu de
+ pour faire la table de multiplication. Table d'addition complète Désignez la cellule et tirez la poignée vers le bas. Désignez la
colonne et tirez la poignée vers la droite. La table est finie.
|
|||
|
Brèves associées |
>>>
Calculatrice >>>
Extraire les chiffres avec tableur |
>>>
Brèves Méthodes – Index |
||
|
Pour en savoir plus |
>>>
Tableur – Index >>> Autres outils |
>>>
Addition |
||
212.
Longueur d'un nombre
|
|
|||
|
Quantité de chiffres d'un nombre Le
logarithme décimal d'un nombre
indique la longueur du nombre. Plus précisément: la quantité de
chiffres dans un nombre entier est égale à la valeur
plafond du logarithme décimal du nombre.
Tableur
Programmation (ceiling = plafond en anglais)
Autre possibilité si le logiciel convertit les nombres en base 10
("nops" donne la quantité d'éléments):
|
Exemples de calculs Le
logarithme de 50 est 1,69… Le nombre
immédiatement supérieur est 2 qui représente la quantité de chiffres dans le
nombre 50.
|
|||
|
Brèves associées |
>>> Mes
tous premiers programmes |
|||
|
Pour en savoir plus |
>>>
Logarithmes |
>>>
Programmation – Débutant >>>
Programmation – Index |
||
213.
Origine du X pour l'inconnue
|
|
|||
|
Diophante, mathématicien du
IIIe siècle, nommait l'inconnue arithmos, le nombre. Al-Khawarizmi, au IXe
siècle, l'appelle SHAY, la chose. De
AL-SHALAN, la chose inconnue. Les Andalous, alors sous
influence arabe, transcrivent en latin: XAY. Le SH pour le son CK n'existait
pas. Le plus proche est le khi grec, écrit
X. On parle aussi de SHEI converti en XEI. Même origine que le CHOUÏA, connu
en français.
|
René Descartes, au XVIIe
siècle, ne conserve que l'initiale. En fait, nul ne sait d'où il tire cette
lettre X. Ce dont on est sûr c'est qu'il est bien à l'origine de sa
popularité. Il utilise les lettres minuscules du début de l'alphabet pour les
quantités connues et celles de la fin pour les inconnues. Ces notations
apparaissent dans ses manuscrits dès 1629. Il introduit également la notation
des puissances comme x3. Une histoire raconte que le
linotypiste de Descartes lui aurait demandé de choisir x, car c'est une
lettre peut employée, et donc plus disponible dans ses casiers de caractères. Il est tout à fait possible
que Descartes ait fait lui-même un choix dans l'alphabet. |
|||
|
Brèves associées |
>>> Les 23
problèmes de Hilbert |
|||
|
Pour en savoir plus |
>>>
Lettre X dans l'alphabet des mathématiques >>>
Alphabet grec |
>>>
Diophante >>>
Al-Khawarizmi >>>
René Descartes |
||
214.
Multiplication par 111
|
|
|||
|
|
On sait
facilement multiplier par 11:
123 x 11 = 1353. On garde les nombres extrêmes (1 et 3) et au milieu, on effectue
l'addition des chiffres deux à deux (1+2 = 3 et 2+3 = 5. On tient compte des
retenues éventuelles. La
multiplication par 111
(1 111, 11 111, etc.) se prête à l'opération à trous indiquée. Pour retrouver
le multiplicateur (cdu: centaines, dizaines et unités), il suffit de
connaitre les trois derniers chiffres du résultat (CDU). Cette
opération à trous peut être organisée en tour de magie. |
|||
|
Unité |
L'unité u
est conservée: u = U = 9 |
|||
|
Dizaine |
La dizaine
d est le nombre qui ajouté à u donne D: d = D – u = 5 – 9. La différence est
négative. On se souvient du mécanisme des retenues. Il suffit d'ajouter une dizaine pour obtenir un nombre positif: 15 – 9 = 6. |
|||
|
Centaine |
La
centaine c est telle que : C = c + d + u, aux retenues près. Or, la
retenue provenant du calcul des dizaines est celle provenant de d + u = 15,
soit 1. Soit, le
calcul: c = C – d – u – r = 9 – 6 – 9 – 1. Avec des dizaines
suffisantes pour que la différence soit un chiffre positif. On
calcule alors: c = 19 – 6 – 9 – 1 = 3 |
|||
|
Bilan |
L'opération
est donc: 111 x 369 = 40
959 |
|||
|
Brèves associées |
>>> Multiplication de nombres entiers >>>
Multiplication par 11, 111, … |
|||
|
Pour en savoir plus |
>>>
Multiplication par un repunit (tour de magie) |
>>>
Nombre 111 |
||
215.
La
fourmi sur le cube
|
|
|||
|
Cube Sur de cube de 4 cm de côté
une fourmi se déplace de E à C en passant par le point M. Quelle est la
position du point M que va viser la fourmi pour minimiser son trajet ? Trajet Avec le théorème de Pythagore
Point M Les trajets sur chacun des
deux carrés successifs doivent se ressembler. Si la fourmi fait le trajet à
contresens, elle visera un point identique à celui qu'elle à visé sur son
trajet aller. Le point M se trouve au
milieu de BF. Avec x = 2, l'expression de la longueur est bien symétrique:
Trajet de la fourmi représenté sur le patron du cube
|
Cube et trajet de la fourmi
Graphe de la fonction EMC
|
|||
|
Brèves associées |
>>> Théorème de Pythagore |
>>> Billard
d'Alhazen |
||
|
Pour en savoir plus |
>>>
Fourmi sur le cube |
>>>
Fourmi sur le pavé |
||
216.
Cent en neuf chiffres
|
|
|||
|
Jeu qui consiste à utiliser tous les chiffres,
dans l'ordre autant que possible, et atteindre le nombre 100 en utilisant les
quatre opérations. Ou, en utilisant des fractions. Beaucoup d'autres possibilités. |
100 = 1 + (2x3) + (4x5) – 6
+ 7 + (8x9) 100 = 1 + 2 + 3 – 4 + 5 + 6
+ 78 + 9 100 = 9 – 8 + 7 + 65 – 4 +
32 – 1
|
|||
|
Brèves associées |
>>> Énigme
des 30 euros |
>>>
Entier manquant |
||
|
Pour en savoir plus |
>>>
Cent en chiffres |
>>>
Jeux avec les nombres |
||
217.
Courbes elliptiques
|
|
|||
|
Définition La courbe
est définie par une fonction du type (équation de Weierstrass). y2 = x3 + Ax + B Notez: pas de
x² Propriété Il se trouve (et on peut le démontrer) que: une
droite sécante passant par deux points de la courbe (P et Q) recoupe la
courbe en un troisième point R (distinct ou non). Addition L'addition est définie de sorte que les
propriétés de l'addition soient réunies: On choisit le point S, symétrique de R (de même abscisse, mais
d'ordonnée opposée). La figure montre la construction qui est ainsi
très simple. |
Exemple de courbe elliptique et Principe de l'addition de deux
points Courbe y2 = x3
– 5x + 8
|
|||
|
Pour en savoir plus |
>>>
Courbes elliptiques |
>>>
Rang des courbes elliptqiues |
||
218.
Logarithmes
|
|
||
|
Approche Un mot
bizarre pour qualifier une notion pas si difficile à comprendre: En
écrivant: 1 000 000 = 106 je fais des logarithmes.
En effet, le nombre 6 est le logarithme de un million. 1 000 000 = 106
et 6 = log (1 000 000) 100 000 = 105
et 5 = log (100 000) Extension Et 5,5,
par exemple, c'est le logarithme de quel nombre? Nous y voilà! Les
mathématiciens ont créé une manière de répondre à cette question. 5,5 = log (316
227,7660) 5,6986… = log
(500 000) |
Intérêt C'est une manière de manipule de grands nombres
représentés par de petits nombres. Mais surtout, l'addition de logarithmes équivaut
à la multiplication des nombres. Ex : 106 x 105 = 1011 et en log 6 + 5 = 11 Pratique pour des multiplications compliquées.
Exemple simple: 123 x 456 => 2,09 + 2,658 = 4,748 => 56
088 Quantité de chiffres dans un nombre
Ex: n = 123456; log(n) = 5,09 |
||
|
Pour en savoir plus |
>>>
Logarithmes >>>
Décibels |
>>>
Quantité de chiffres >>>
Plancher, plafond … |
|
219.
Magie – Nombre deviné
|
|
|||
|
Question Pensez à un nombre n inférieur à 60 et donnez-moi
simplement le reste de la division par 3, par 4 et par 5, disons a, b et c. Je devine le nombre Je calcule secrètement: S = 40a + 45b + 36c Le nombre n est égal au reste de la division de S
par P = 60 = 3 x 4 x 5. Exemple Si n = 57,
alors: a = 0, b = 1 et c = 2. S = 40x0 + 45x1 + 36x2 = 117 =
1 x 60 + 57 |
Calcul des coefficients 60 = 3 x 4 x 5 le produit
des trois diviseurs 40 est le plus petit
multiple de 4 x 5 tel que, diminué de 1, il est divisible par 3. 45 est le plus petit
multiple de 3 x 5 tel que, diminué de 1, il est divisible par 4. 36 est le plus petit
multiple de 3 x 4 tel que, diminué de 1, il est divisible par 5. Avec quatre nombres P = 3 x 4 x 5 x 7 = 420, alors: S = 280a + 105b+
336c + 120d D'après Bachet
de Méziriac – Problèmes
plaisans et délectables |
|||
|
Brèves associées |
>>> Âge
répété >>> Somme
d quatre carrés |
>>>
Preuve
par 9 et sa magie |
||
|
Pour en savoir plus |
>>>
Tour de magie avec 60 |
>>>
Restes chinois – Problème de Sun Zi |
||
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()