|
Édition du: 30/07/2022 |
|
INDEX |
Géométrie intrigante |
||
Faites un double-clic pour un retour en haut de page
![]()
|
Problème de KAKEYA ou de l'aiguille qui tourne
Faire faire un
tour complet à une aiguille en balayant l'aire minimale. L'aiguille ne peut
que glisser ou tourner tout en restant dans le plan. Quelle est la
valeur de cette aire minimale ? L'aire du disque. Pas si simple; il y a
mieux, nettement mieux …
|
||
|
|
Sommaire de cette page >>> Le problème de l'aiguille de Kakeya >>> Solution du deltoïde >>> Solutions des fils tendus >>> Jonction de Pal >>> Construction de Besicovitch >>> De 1919 à 2008 – La solution Besicovitch >>> Solutions modernes: 2008 à 2022 |
Débutants Glossaire |
|
Disque Une aiguille de longueur unité. Elle doit faire un tour complet dans le plan. Si on fait pivoter l'aiguille autour de son
centre, la surface balayée est un disque.
Est-ce que l'aire balayée est la plus petite ? |
Solution la plus évidente. |
|
|
Triangle de Reuleaux (cercle "aplati") Le triangle
de Reuleaux est connu. Avec sa
forme arrondie, il permet notamment la construction de moteur rotatif. Pour sa construction, on utilise un triangle
équilatéral et, sur chaque côté, on dessine le segment de cercle avec le
sommet opposé comme centre et la longueur du côté comme rayon. L'aiguille tourne d'un sixième de tour (60°)
autour d'un des sommets et, ayant atteint un autre sommet, elle se met à
tourner à partir de ce sommet, etc. |
Solution qui diminue l'aire de la surface balayée
par l'aiguille. |
|
|
Triangle équilatéral Pourquoi conserver les bords arrondis ? Avec un triangle équilatéral ayant la longueur de
l'aiguille pour hauteur (1), on balaye selon le sixième de tour matérialisé
en pointillés, passant de position 0 à la position 2. Puis, une translation
le long du côté permet de passer en position 3 et de poursuivre en balayant
sur un nouveau tiers de tour. Etc. En 1921, le mathématicien hongrois Julius Pal (1881-1946) démontre
qu’il n’existe pas de domaine convexe plus
petit que le triangle
équilatéral et qui autorise le retournement de l’aiguille. |
Meilleure solution
"convexe"
Encore un nouveau gain. Est-ce la limite ? Oui, pour une surface convexe;
non dans le cas général. |
|
|
|||
|
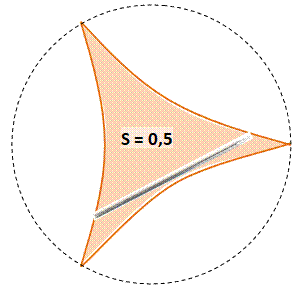
Deltoïde La deltoïde
est la trajectoire d'un point d'un cercle lorsque celui-ci roule sans glisser
à l'intérieur d'un cercle trois fois plus grand. L'aiguille tourne avec ses deux extrémités
parcourant deux arcs tandis qu'elle reste tangente au troisième arc.
Conjecturant que c'était la meilleure
solution, les mathématiciens
essayèrent de prouver qu'il s'agissait de la surface minimale, sans vraiment
chercher mieux. Puis … |
Meilleure solution "non- convexe"
? On l'a longtemps cru !
Cette fois, avec cette solution, on doit tenir la
limite ! |
||
Voir Brève
917
|
Fils tendus sur axes perpendiculaires Pourtant, une nouvelle technique originale est
possible: les extrémités de l'aiguille glissent à la fois sur deux axes
perpendiculaires. Pou réaliser le tour complet, il faut quatre fois
cette figure. Il est possible d'optimiser en utilisant une autre valeur d'angle. Ci-dessous, un
angle de 120°. |
L'enveloppe des droites est une hyperbole. |
||
|
Angles plus grands Motif élémentaire et regroupement, ici, par trois pour faire le tour complet. L'analyse de ces cas montre qu'à partir de l'étoile à treize branches
l'aire balayée est inférieure à 0,5. En augmentant la quantité l'aire décroit
encore puis se met à croitre. |
Une solution encore meilleure de la deltoïde avec
environ quinze branches. |
||
|
Rotation de l'aiguille On va prendre une image avec un train (figuré en bleu) qui remontre les
rails vers un aiguillage et recule sur la voie d'à côté. Cette opération fait tourner le train d'un angle
alpha et cela en balayant la petite surface rouge. En reproduisant cette opération en cercle, on
peut faire tourner le train de 360°. En diminuant l'angle, la surface rouge tend vers 0 et même
en multipliant par une infinité
d'aiguillages, l'aire devrait être voisine de zéro. Eh bien NON ! Voir Zéro
x Infini = indéterminé |
Le principe général
Le segment bleu navigue dans cette ligne en V. Il
tourne d'un angle alpha en balayant la
seule surface rouge, aussi petite que l'on veut en réduisant l'angle. L'aire
du secteur vaut C'est l'aire du secteur unité. Donc, pas la bonne solution ! Mais le principe est le
bon. |
||
|
Construction de Julius Pal Changement de tactique: on cherche une méthode
pour passer d'une droite à sa voisine qui lui est parallèle. On montre que ce double aiguillage, conduit à une
aire balayée (rouge) aussi pette que l'on veut, car: |
|
||
|
Bilan: jonction de Julius Pal Étant donné deux lignes parallèles, un segment peut
passer de l'une à l'autre avec une surface d'aire aussi petite que l'on veut.
Sur l'illustration, la surface verte suffit. |
|
||
|
Ensembles (ou figures) de
Besicovitch (1891-1970)
|
Inventé pour montrer que le retournement de
l'aiguille peut être réalisé dans une surface d'aire aussi petite que l'on
veut. Ce sont des figures dont la petitesse est sans
limite mais qui permettent toutes le retournement de l'aiguille. |
||||||||
|
Construction de Besicovitch Dans un premier temps on balaye un secteur aussi
petit que l'on veut. Sans autre procédé on aboutit à une surface balayée dont
l'aire est celle du disque. L'astuce consiste à partager le secteur en deux
et à les superposer. Alors, on sait balayer dans chacun des secteurs et
l'aire balayée est plus petite que celle du secteur initial, voire proche de
zéro si on diminue la taille du secteur. Mais comment passer d'un demi-secteur à l'autre ?
Avec le procédé de Pal ! |
|
||||||||
|
Combinaison des deux opérations Répétée sur un tour, ces opérations permettent la
rotation complète de l'aiguille pour une surface balayée aussi proche de zéro
que l'on veut. |
Assemblage des secteurs (exemple)
|
||||||||
|
Pour minimiser la surface balayée, Besicovitch va
plus loin. Au lieu de partager en deux, il partage en quatre
ou même plus. Il regroupe ces lamelles en gerbes au niveau du pied, puis par
le milieu et encore plus haut, puis … On montre que l'aire obtenue est la moitié de
celle du départ avec quatre étages et
diminue avec plus d'étages. |
Réduction de l'aire par le facteur que l'on veut en augmentant la
quantité de regroupements par étages. |
||||||||
|
Le résultat est un arrangement fractal complexe
avec une zone qui peut être rendue arbitrairement petite, ce qui équivaut à
n'avoir aucune aire du tout. |
|||||||||
|
Aire pratiquement nulle ! Dès 1928*, Abram Besicovitch démontre qu'il n'y a
pas de limite. * Études réalisées dès 1919 indépendamment de
Kakeya et publiées en 1928. L'aire peut être aussi proche que l'on veut de zéro
sans être nulle. Sa démonstration utilise un principe très particulier de son invention associé aux jonctions de Pal. La méthode de construction itérative qui rend l'aire
aussi petite que l'on désire s'appelle l'arbre de Perron. |
La méthode utilisée par Besivovitch est expliquée
dans le livre
de Borelli et Rullière – page 111 et suite. |
|
|
Ensemble de Kekaya ou de Besicovitch Ensemble de points d'un espace euclidien qui
contient un segment de droite de longueur unité dans chaque direction. Conjecture de Kakeya Elle porte sur la taille minimale des ensembles
de Kekaya en dimension quelconque. Cette conjecture annonce que l'ensemble de Kekaya
doit avoir une dimension
(fractale) minimale en fonction de n au sens Hausdorff ou Minkowski. La preuve existe pour n = 2 (le plan) et la
propriété est toujours à démontrer pour n supérieur. |
Un ensemble de Kakeya construit avec l'arbre de
Perron "À la limite, c'est une chose étrange qui
ressemble à un hérisson" dit Zeev Dvir, auteur de
nouvelles preuves à Princeton |
|
|
Zeev Dvir, mathématicien et informaticien à
l'Université de Princeton, a prouvé la conjecture de Kakeya pour certains
systèmes de nombres finis avec son étudiant, Manik Dhar. |
Zeev Dvir et
Manik Dhar |
|
|
L'ensemble de Besicovitch est formé d'un ensemble
de points. Comment sont-ils répartis ? Pour poursuivre les investigations, la notion
d'aire n'est pas suffisante. Approche (caractérisation) via la notion de
dimension fractale (Hausdorff et Minkowski). |
La conjecture de Kakeya prédit que les dimensions
de Hausdorff et de Minkowski d'un ensemble de Kakeya doivent être aussi
grandes que possible. |
|
|
Nombres premiers La piste des ensembles de Kakeya pour
étudier les nombres
premiers n'est pas évidente. |
Il s'agit essentiellement de travailler sur la
répartition des nombres premiers, caractérisée par des progressions
arithmétiques. |
|
|
Nombres réels Le fait que l'aire s'approche de zéro sans
l'atteindre fait penser aux nombres
rationnels que l'on peut rendre très proche d'un nombre réel
mais sans l'atteindre. Voir Coupure de Dedekind L'arithmétique
modulaire semble un axe de recherche prometteur. |
Difficultés:
les nombres réels sont en quantité infinie
non-dénombrable. Ils remplissent continument la droite des nombres. En 2008, Zvir a résolu la conjecture de Kakeya
dans le système de nombres congruents dont le module est premier. En 2020, Zvir et Dhar tendent la démonstration aux
nombres composés produit de deux premiers.
Ils utilisent une représentation matricielle: points en colonnes et
directions en lignes. Les propriétés trouvées pour cette matrice seront
celles de l'ensemble. Ils ont montré qua la taille de la matrice est
nécessairement très grande. |
|
|
Les mathématiciens explorent cette piste, aussi
avec l'outil des nombres p-adiques,
pour parfaire les connaissances en théorie des nombres. |
En 2021, Bodan Arsovski (université de Londres) étend
la preuve de la conjecture pour les nombres
premiers portés à une puissance. Son outil, les nombres p-adiques. |
|
|
Derniers développements La conjecture de Kakeya est démontrés pour les
nombres discrets dans divers systèmes. Elle reste ouverte pour les nombres réels. Certains mathématiciens doutent qu'elle soit
vérifiée dans ce cas-là. |
En octobre 2021, Dhar prouve la conjecture de
Kakeya pour tout module, premiers comme composés. En 2022, Salvatore prouve la conjecture pour les corps
locaux (localement compact) à caractéristique positive. |
|
Source: certaines illustrations proviennent
du livre indiqué en référence
La
vision moderne est insprirée du texte de Kevin Hartnett de
juillet 2022
Avertissement
|
Comme
c'est habituel avec ces pages, le sujet est volontairement traité de façon simple,
abordable par une majorité d'internautes. Pour un
traitement plus mathématique, se reporter aux nombreux sites internet, surtout
en anglais, dont de nombreuses vidéos. Je
recommande le livre et la vidéo de Vincent Borelli et als. |
Anglais
|
Take a needle and rotate it all the way around. What’s the smallest
area that you can cover? Kakeya was curious about the smallest area required in the
two-dimensional plane to turn a one-dimensional line of a given length so
that it eventually points in all
directions The Kakeya conjecture predicts how much room you need to point a line
in every direction. |
Voir
Anglais pour le bac et pour les affaires
![]()
|
Retour |
||
|
Suite |
||
|
Voir |
|
|
|
|
||
|
Sites |
|
|
|
Cette page |
||