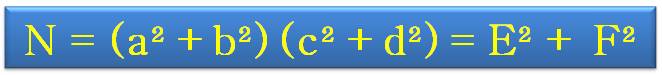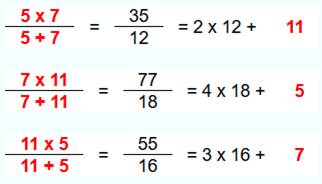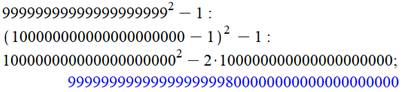NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 03/10/2024 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Maths en se divertissant
Débutants Général	BRÈVES de MATHS									Glossaire Général
INDEX Brèves Atlas des maths	Page 1	Page 10		Page 20		Page 30		Page 40			Page 50
	Page 10 (180-199)		Page 11 (200-219)		Page 12 (220-239)		Page 13 (240-259)		Page 14 (260-279)
	Page 15 (280-299)		Page 16 (300-319)		Page 17 (320-339)		Page 18 (340-359)		Page 19 (360-379)

BRÈVES de MATHS – Page 18

Un millier de faits et chiffres

sur les nombres et les mathématiques

Ces pages sont dédiées à tous ceux qui veulent aborder les mathématiques en douceur et en s'amusant tout en découvrant les aspects les plus fondamentaux de cette discipline. Un parcours à picorer avec nombreux liens d'orientation vers les développements destinés à satisfaire votre curiosité.

En principe ces pages sont très abordables sans connaissances particulières de maths. Elles sont proposées dans un ordre quelconque favorisant la découverte de sujets multiples.

Anglais: Facts and figures about numbers and mathematics

340. Identité d'un nombre entier

Un nombre entier est caractérisé principalement pas son développement en facteurs premiers.

Le théorème fondamental de l'arithmétique dit que le développement en facteurs croissants est unique.

L'énumération de ses diviseurs et leur quantité est une conséquence de la factorisation: ce sont tous les produits des facteurs entre eux.

La somme complète ou sans le nombre lui-même est utilisée pour déterminer si un nombre est déficient, parfait ou abondant.

Facteurs	60 = 1 x 2² x 3 x 5
Diviseurs	1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60
Quantité	12
Somme	1 + 2 + 3 + … + 60 = 168
S - N	168 – 60 = 108

Le nombre 60 est abondant car la somme des diviseurs propres (108) est supérieure au nombre 60.

Brèves associées

>>> Nombres abondants, déficients et parfaits

>>> Nombres 0 et 1

Pour en savoir plus

>>> Théorème fondamental de l'arithmétique

>>> Nombre entier

341. Nombre 60
Carte d'identité Voir La brève ci-dessus Ses diviseurs La principale propriété du nombre 60 est qu'il possède une grande quantité de diviseurs dont tous de 2 à 6. Ce qui explique son choix comme base de numération par les Mésopotamiens. Avec lui, il est possible de former de nombreuses fractions pratiques pour un usage dans la vie de tous les jours. Le nombre 60 est super-abondant. Aucun nombre plus petit n'a une somme de diviseurs aussi grande (168). La somme juste inférieure est 124, somme des diviseurs de 48.		Sa nature 60 est un nombre pair, divisible par 2. 60 est un nombre composé. 60 est un nombre multipronique. Il est le produit de nombres sans puissance: 60 = 3 x 4 x 5 60 est un nombre d'Harshad. Il est divisible par une combinaison de ses chiffres: 60 / (6 + 0) = 10. Propriétés Comme tout produit de trois nombres consécutifs dont le central est en 4k, 60 est divisible par 12. L'angle de 60° est l'angle du triangle équilatéral.
Brèves associées	>>> Nombre 100 >>> Nombre 2019		>>> Nombres de Harshad >>> Nombre pronique
Pour en savoir plus	>>> Nombre 60 (DicoNombre) >>> DicoNombre – Portail		>>> Divisible par 12 >>> Nombres multi proniques

342. Rectangle partagé
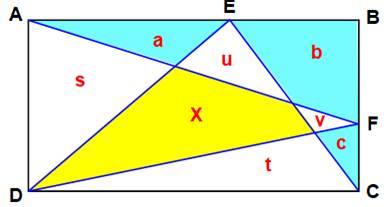
Énigme Un rectangle ABCD et deux points E et F quelconques sur AB et BC. Que peut-on dire de la surface jaune par rapport à celles en bleu ? Indice L'aire d'un triangle inscrit dans un rectangle (comme ADF ou DEC) est égale à la moitié de l'aire (R) du rectangle.
Brèves associées	>>> Trois souris sur triangle		>>> La fourmi sur le cube
Pour en savoir plus	>>> Rectangle partagé – Solution		>>> Rectangle – Énigme

343. Programmes et pages Internet
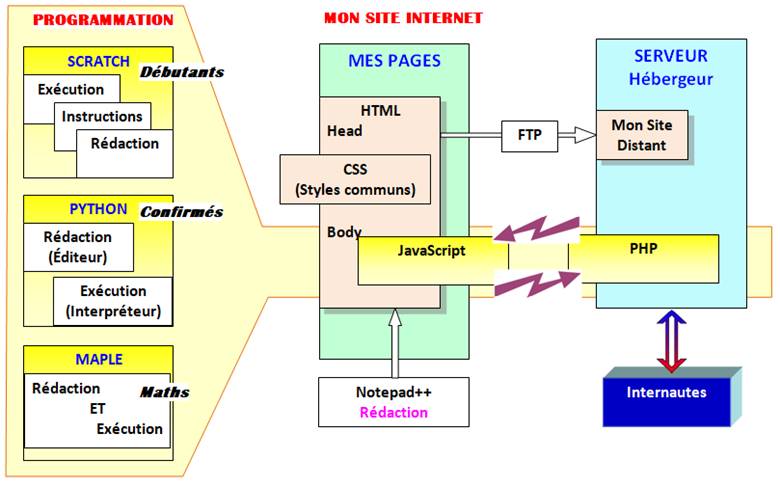
Jaune: des langages de programmation qui se ressemblent. Vert: les fichiers de mon site Internet Bleu: chez mon fournisseur d'accès (Orange, Free, autres)
Brèves associées	>>> Pages sur l'informatique: binaire, ordinateurs, loi de Moore, etc.
Pour en savoir plus	>>> Outils de programmation avec explication de ce graphique

344. Multiplication – Somme unités = 10
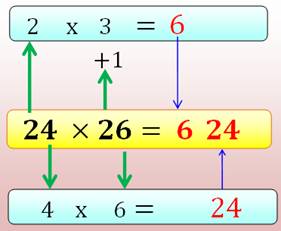
Un exemple (illustration) Voyez cette multiplication: 24 x 26 = 624. Elle marche à tout coup lorsque: Le chiffre des dizaines est le même, et La somme des chiffres des unités est égale à 10. Autres exemples 82 x 88 = 72 16 avec 8 x (8+1) = 72 et 2x8 = 16 95 x 95 = 90 25 12 x 18 = 2 16 Note: si le produit des unités ne dépasse pas 10, placer un 0 intercalaire. 11 x 19 = 2 09 avec = 1 x 2 = et 1 x 9 = 9 91 x 99 = 90 09		Calcul rapide de 26 x 24 = 624 Justification (10d + u) (10d + (10-u) ) = 100d(d+1) + u(10–u)
Brèves associées	>>> Multiplication de nombres proches de 100 >>> Multiplication rapide à pivot
Pour en savoir plus	>>> Multiplications avec 10 pour somme des unités		>>> Calcul mental – Index

345. Multiplication par 11, 111
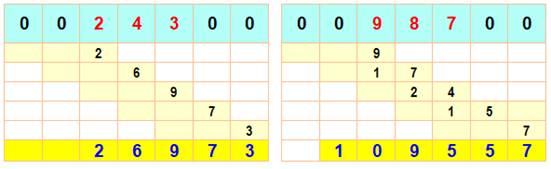
Multiplication par 11 Entourez le nombre par deux 0 (par la pensée). Calculez chaque chiffre en effectuant la somme sur une fenêtre glissante de deux chiffres. Tenez compte des retenues éventuelles.
Multiplication ² par 111 Même principe avec une fenêtre glissante de trois chiffres.
Brèves associées	>>> Multiplication de nombres proches de 100 >>> Multiplication rapide à pivot >>> Multiplication à trous avec 111
Pour en savoir plus	>>> Multiplications par 11 et autres avec 11			>>> Calcul mental – Index

346. Addition mentale
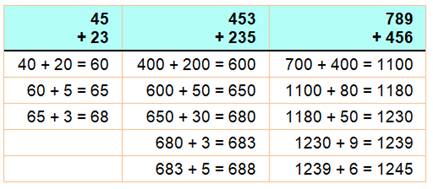
Le but est d'obtenir en premier les chiffres les plus "forts" (ceux à gauche), contrairement au calcul classique de l'école. Alors je commence à gauche et je récite mentalement les lignes indiquées ci-contre dans le tableau: 40 + 20 = 60 puis 60 + 5 = 65 et enfin 65 + 3 = 68. Etc. Bénéfice: le problème de la propagation de la retenue est éliminé.		Exemples d'additions à effectuer mentalement Méthode adaptée pour addition de plusieurs nombres, mais vite délicate pour de grands nombres.
Brèves associées	>>> Addition de nombres entiers >>> Multiplication – Truc de calcul mental
Pour en savoir plus	>>> Addition – Truc de calcul mental >>> Soustraction – Truc de calcul mental >>> Addition 27 + 48 – Tous les trucs possibles		>>> Calcul mental – Index

347. Cubes et divisibilité par 6

La différence entre deux cubes successifs moins 1 est divisible par 6.

Calcul avec identité remarquable:
(n + 1)³ = n³ + 3n² + 3n + 1

En retirant les extrêmes:

3n² + 3n = 3 n (n + 1)

Parmi deux nombres consécutifs l'un est pair. Leur produit est divisible par 2.

L'ensemble est divisible par 2 et 3, donc par 6.

Propriété

T_n est le nombre triangulaire de rang n.

Exemples

2^3	– 1^3	– 1 =	8 –	1	– 1 =	6 =	1 × 6
3^3	– 2^3	– 1 =	27–	8	– 1 =	18 =	3 × 6
4^3	– 3^3	– 1 =	64 –	27	– 1 =	36 =	6 × 6
5^3	– 4^3	– 1 =	125 –	64	– 1 =	60 =	10 × 6
6^3	– 5^3	– 1 =	216 –	125	– 1 =	90 =	15 × 6
7^3	– 6^3	– 1 =	343 –	216	– 1 =	126 =	21 × 6
8^3	– 7^3	– 1 =	512 –	343	– 1 =	168 =	28 × 6
9^3	– 8^3	– 1 =	729 –	512	– 1 =	216 =	36 × 6
10^3	– 9^3	– 1 =	1000 –	729	– 1 =	270 =	45 × 6
11^3	– 10^3	– 1 =	1331 –	1000	– 1 =	330 =	55 × 6

Brèves associées

>>> Divisibilité avec des factorielles

Pour en savoir plus

>>> Divisilité par 6

>>> Divisilité de formes polynomiales

>>> Nombres triangulaires

>>> Nombre 6

348. Multiplication magique par 91
Table de 9		Multiplication magique		Calcul On fait la multiplication classique par 9 et on adjoint le multiplicateur à la fin Explication Une multiplication par 91 revient à multiplier par 100 et à retrancher le produit par 9. Ex: 2 x 91 = 2 (100 – 9) = 200 – 18 = 182 Il n'est pas étonnant de retrouver la forme incrémentale des chiffres due à la multiplication par 9.
Brèves associées	>>> Preuve par 9 et sa magie		>>> Carré magique à la demande
Pour en savoir plus	>>> Nombre 91 >>> Divisibilité par 91		>>> Carte postale 2102 >>> Magie – Index

349. Identité de Brahmagupta
Exemples 50 = (1² + 2²) (1² + 3²) = (1² + 7²) 65 = (1² + 2²) (2² + 3²) = (1² + 8²) 68 = (1² + 1²) (3² + 5²) = (2² + 8²)		Propriété Tous nombre somme de deux carrés peut être transformé en produit de deux sommes de carrés. Plus précisément (a² + b²) (c² + d²) = (ac – bd)² + (ad + bc)² (1² + 2²) (3² +4²) = (1.3 – 2.4)² + (1.4 + 2.3)² = 5² + 10²
Brèves associées	>>> Identités remarquables		>>> Amusement avec les carrés
Pour en savoir plus	>>> Identité de Brahmagupta >>> Nombre 125		>>> Carte postale 2104

350. Puissance de 2 moins 1
Défi Trouver les facteurs de 2^16 – 1 sans effectuer le calcul Calcul 2^16 – 1 = 65 535 = 5 x 13 107 = 5 x 3 X 4 369 = ? Suite, pas simple !		Autre méthode Un petit changement d'écriture et une identité remarquable: 2^16 – 1 = 2^16 – 1^16 = (2^8 + 1^8 ) (2^8 – 1^8) = 257 x (2^8 – 1^8 ) On continue … = 257 x (2^4 + 1^4) (2^4 – 1^4) = 257 x 17 x (2^4 – 1^4) = 257 x 17 x (2^2 + 1^2) (2^2 – 1^2) = 257 x 17 x 5 x 3
Brèves associées	>>> Identités remarquables		>>> Diviseurs d'un nombre >>> Modulo – Divisibilité par 5
Pour en savoir plus	>>> Nombre de Mersenne: 2^n – 1		>>> Carte postale 2213

351. Fractions en boucles
Motif en boucle avec des divisions et seulement trois nombres. Un recherche par exploration ou par calcul montre que ce triplet {5, 7, 11} est le seul original à disposer de cette propriété, sauf un triplet trivial (anodin) formé de trois 1: {1, 1, 1}. Original, ici veut dire: nombres entiers positifs et tous premiers entre eux.		Bouclage avec les nombres5, 7 et 11
Brèves associées	>>> Fraction et série infinie		>>> Puissances et divisibilité par 5
Pour en savoir plus	>>> Fractions illicites		>>> Carte postale 2216

352. Produit de nombres proches
Deux nombres (n) et (n – 1) Le produit de deux nombres consécutifs est égal au carré du plus grand diminué de ce nombre. 6 x 7 = 7² – 7 11 x 12 = 12² – 12		Deux nombres (n – 1) et (n + 1) Le produit de deux nombres espacé de 2 unités est égal à au carré du nombre intermédiaire moins 1. 6 x 8 = 7² – 1 10 x 12 = 11² – 1
Brèves associées	>>> Addition – Truc de calcul mental >>> Multiplication rapide – Méthode générale
Pour en savoir plus	>>> Calcul mental des carrés		>>> Calcul mental – Index

353. Calcul mental du cube
Pour calculer le cube de n, faire le produit des trois nombre consécutifs centrés sur n et ajouter n. Dans certains cas, il est plus facile de faire cette opération plutôt que les deux multiplications habituelles.
Brèves associées	>>> Multiplication mentale – le truc général
Pour en savoir plus	>>> Calcul du cube	>>> Cubes

354. Bouliers
Boulier chinois ou Suan Pan Chaque colonne représente les dizaines successives comme avec nos nombres classiques. Chaque jeton en bas vaut 1 et chacun en haut vaut 5.		Boulier japonais ou Soroban Même principe pour ce boulier, qui ne comporte que quatre jetons en bas et un seul en haut. Avec celui-ci, il est facile d'effectuer une transposition à la main: le pouce vaut 5 et les quatre autres doigts valent 1 chacun. Une méthode de calcul mental avec les doits utilise ce principe.
Brèves associées	>>> Tableur		>>> Calcul mental des cubes
Pour en savoir plus	>>> Bouliers		>>> Soroban et calcul avec les doigts

355. Carré = somme de cubes
Exemples de lecture et explications 4^3 = 64 = 8² 9^3 = 729 = 27² Deux nombres à la fois cubes et carrés 1^3 + 2^3 = 9 = 3² = (1 + 2)² 1^3 + 2^3 + 3^3 = 36 = 6² = (1 + 2 + 3)² La somme des cubes des nombres consécutifs de 1 à n est égale au carré de la somme des nombres de 1 à n. 4^3 + 8^3 = 576 = 24² = (1 + 23)² = … 1^3+ 2^3 + 6^3 = 225 = 15² = (2 + 13)² = … Il existe des cas où, la somme de cubes quelconques est égale à un carré. Il est aussi égal au carré de toutes les partitions de la racine de carré (évident).
Brèves associées	>>> Carré = cube		>>> Carré et cube à la fois
Pour en savoir plus	>>> Carré = Somme de cubes

356. Calcul du carré d'un nombre à trois chiffres
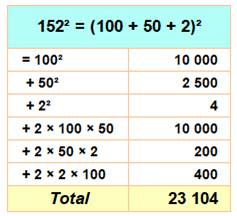
Identité (a + b + c )² = a² + b² + c² + 2ab + 2bc + 2ca
Brèves associées	>>> Calcul mental des carrés		>>> Carré des nombres en 5
Pour en savoir plus	>>> Calcul mental des carrés		>>> Nombres carrés

357. Hasard
Étymologie En arabe populaire: az-zahr désignait le dé à jouer (le "az" est la forme de "al" remplacée devant "z"). Forme passée par l'espagnol azar, coup défavorable au jeu de dés. Le Moyen Âge ajoute un h, comme c'était souvent l'usage devant les mots à initiale vocalique. Vers 1150, hasart désignait le jeu de dés. De son côté aléa vient du latin: jeu de dés, jeu de hasard. Alea ludere: jouer aux dés. Alea jacta est: les dés sont jetés ou le sort en est jeté. Phrase prononcée par Jules César avant de franchir le fleuve Rubicon, au nord est de l'Italie en 49 av. J.-C.		Limite de nos certitudes La mécanique classique, et toutes ses lois, peut-elle tout prédire comme le pensait Pierre-Simon de Laplace: "une intelligence qui connaîtrait toutes les forces de la nature … Rien ne serait incertain pour elle et l'avenir comme le passé serait présent à ses yeux". Cette prédiction déterministe a été mise à mal lors de la découverte des phénomènes chaotiques. La moindre différence de conditions initiales caractérisant un phénomène peut l'entrainer sur des routes totalement différentes. La mécanique quantique nous révèle qu'un phénomène est dans plusieurs états à la fois et que c'est son observation qui impose la concrétisation en un état plutôt qu'un autre. Le hasard est loin d'être maitrisé !
Brèves associées	>>> Jeu de dés		>>> Anniversaire le même jour
Pour en savoir plus	>>> Hasard >>> Probabilités		>>> Chaos >>> Physique quantique (le chat …)

358. Grenouilles sauteuses
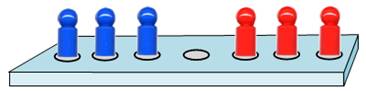
Le jeu consiste à faire passer les pions bleus à la place des rouges, et les rouges à la place des bleus. Règle du jeu Les pions avancent vers leur nouvelle destination et ne repartent jamais en arrière. Un pion avance vers une place libre devant lui ou saute par-dessus un pion pour atteindre la place libre juste derrière.		La solution optimale nécessite 15 mouvements.
Brèves associées	>>> Labyrinthes		>>> Énigme du parking
Pour en savoir plus	>>> Grenouilles sauteuses >>> Tour de Hanoï		>>> Jeux et énigmes – Index

359. Motif itératif en 99 et 98
Comment calculer simplement : 999..9² – 1, sachant qu'il y a vingt fois le chiffre 9. Il suffit de prendre 99² – 1 et de le mettre sous la forme (100 – 1)² - 1. En développant le carré on obtient: (100² – 2 x 100 + 1) – 1 = 200² - 200 = 9800. En poursuivant, on découvre la règle de composition du résultat. (Voir Tableau) Pour 20, on trouvera immédiatement:
Brèves associées	>>> Palindromes		>>> Pépites numériques
Pour en savoir plus	>>> Repdigit en 9		>>> DicoNombre 9 800

Retour	Brèves de maths – Page 17
Suite	Brèves de maths – Page 19
Voir	Voir liens en haut de page
Cette page	http://villemin.gerard.free.fr/NombDico/aBreves/Breve18.htm