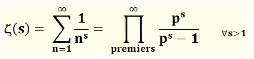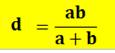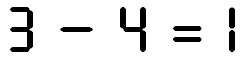NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 15/10/2023 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Maths en se divertissant
Débutants Général	BRÈVES de MATHS									Glossaire Général
INDEX Brèves Atlas des maths	Page 1	Page 10		Page 20		Page 30		Page 40			Page 50
	Page 50 (980-999)		Page 51 (1000-1019)		Page 52 (1020-1039)		Page 53 (1040-1059)		Page 54 (1060-1079)
	Page 55 (1080-1099)		Page 56 (1100-1119)		Page 57 (1120-1139)		Page 58 (1140-1159)		Page 59 (1160-1179)

BRÈVES de MATHS – Page 54

Un millier de faits et chiffres

sur les nombres et les mathématiques

Ces pages sont dédiées à tous ceux qui veulent aborder les mathématiques en douceur et en s'amusant tout en découvrant les aspects les plus fondamentaux de cette discipline. Un parcours à picorer avec nombreux liens d'orientation vers les développements destinés à satisfaire votre curiosité.

En principe ces pages sont très abordables sans connaissances particulières de maths. Elles sont proposées dans un ordre quelconque favorisant la découverte de sujets multiples.

Anglais: Facts and figures about numbers and mathematics

1060. Cercle des neuf points
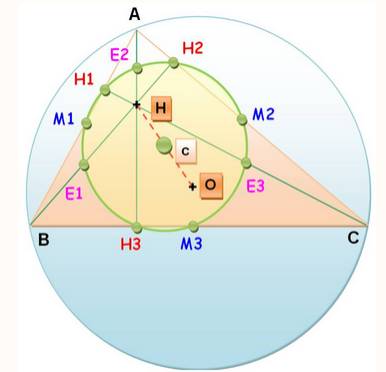
Cercle des neuf points, cercle 'Euler ou cercle de Feuerbach Pour tout triangle ABC, il existe un cercle (vert) qui passe par: le milieu des côtés (M), le pied des hauteurs (H) et le milieu (E) du segment joignant un sommet à l'orthocentre. Le centre de ce cercle (c) est le milieu du segment joignant le centre (O) du cercle circonscrit (bleu) à l'orthocentre (H). Bien d'autres … Depuis, on a dénombré plus de 40 points remarquables sur ce cercle. Et … plusieurs centaines de points remarquables dans un triangle.
Brèves associées	>>> Cercle de Conway		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Cercle des neuf points >>> Orthocentre du triangle		>>> Points remarquables du triangle

1061. Fausse perspective
Tableau de William Hobbarth (1754), intitulé: satire sur la fausse perspective (satire on flase perspective). Lequel affirme: quiconque exécute une œuvre sans la connaissance de la perspective sera passible des absurdités illustrées sur ce frontispice. Le jeu consiste à recenser toutes les erreurs de perspectives visibles sur ce tableau. La page Wikipédia en identifie 25. D'autres sites en dénombrent plus.
Brèves associées	>>> Grenouille et cheval – Illusion		>>> Brèves Divertissements – Index
Pour en savoir plus	>>> Illusions d'optique		>>> Illusions avec la nature

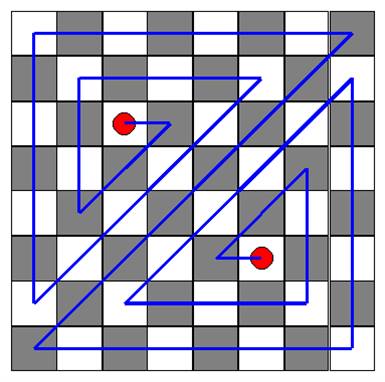
1062. Roméo et Juliette
Problème Roméo doit rejoindre Juliette (points rouges) en un minimum de mouvements tout en passant une seule fois sur toutes les cases de l'échiquier. Solution Possible en 15 déplacements comme illustré ci-contre. Auteur Henry Dudeney (1847-1930) dans Canterbury Puzzles en 1907.
Brèves associées	>>> Roméo et Juliette – Cruche d'eau		>>> Brèves Énigmes – Index
Pour en savoir plus	>>> Roméo et Juliette >>> Jeux de déplacements		>>> Henry Dudeney

1063. Nombres premiers – Propriétés
Propriétés simples Le nombre 2 est le seul premier pair; Aucun premier ne se termine par 5, sauf le nombre 5; Hors (2 et 5), tous les nombres premiers se terminent par 1, 3, 7 ou 9; Le produit de deux premiers n'est jamais un carré ou autre puissance; Hors (2 et 3), tous les nombres premiers sont voisins d'une unité d'un multiple de 6. La conjecture de Goldbach affirme que tout nombre pair (sauf 2) est la somme de deux premiers.		Propriétés avancées (et extraordinaires !) L'ensemble des nombres premiers est relié à l'ensemble des nombres entiers par l'identité d'Euler: La résolution de la conjecture de Riemann conduirait à mieux connaitre la répartition des nombres premiers. Celle-ci consiste à affirmer que tous les zéros non triviaux de la fonction indiquée ci-dessus sont sur la droite 1/2.
Brèves associées	>>> Nombres premiers		>>> Brèves Types de nombres – Index
Pour en savoir plus	>>> Conjecture de Goldbach >>> Hypothèse de Riemann		>>> Nombres premiers – Index >>> Barre magique des premiers

1064. Orbites des planètes
Orbites géocentriques des planètes Trajectoires des planètes telles que vues de la Terre. Sur ces représentations, la Terre est au centre. Source images: Curves of planetary motion in geocentric perspective: Epitrochoids – Animations disponibles
Brèves associées	>>> Magnitude des étoiles	>>> Brèves Astronomie – Index
Pour en savoir plus	>>> Orbites des planètes	>>> Système solaire

1065. Les dix triangles
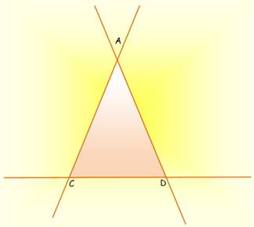
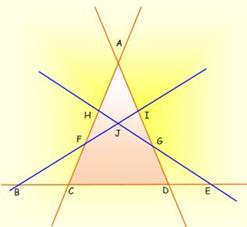
Problème Avec seulement cinq traits, dessiner une figure contenant exactement dix triangles. Variante (Figure du haut) Pour ce jeu, on donne souvent les droites concourantes AC, AD et CD et on demande d’ajouter deux traits pour obtenir dix triangles. Solution (Figure du bas) Tracer les droites BI et EH Nom des dix triangles BCF, FHJ, GIJ, DEG BDI, CEH AIF, AGH ACD, BEJ
Brèves associées	>>> Dix en chiffres		>>> Brèves Énigmes – Index
Pour en savoir plus	>>> Jeux divers avec 10		>>> Jeux divers avec 12

1066. Les huit carrés
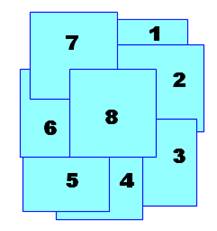
Problème Huit carrés comme celui-ci on été superposés selon la configuration indiquée. Dans quel ordre ont-ils été posés ? Solution La figure en bas montre dans quel ordre il faut disposer les carrés successifs. Vérification On peut découper les carrés dans du carton et vérifier. On peut aussi utiliser un logiciel de dessin comme celui présent dans Word.
Brèves associées	>>> Grenouilles sauteuses		>>> Brèves Énigmes – Index
Pour en savoir plus	>>> Carré parfait		>>> Pavage avec des dominos

1067. Polygones en beauté
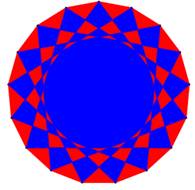
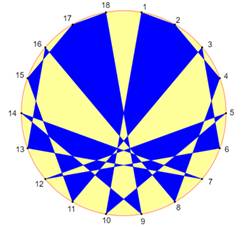
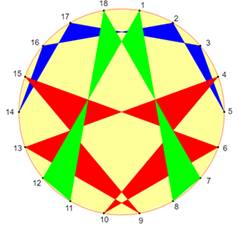
Un point sur k (quatre cercles du haut) Polygone régulier à 17côtés et Polygone formé en joignant un point sur k jusqu'à revenir au point initial (pour fermer le polygone) Avec k = {3, 4, 5, 6} Modulo (trois cercles du bas) Polygone régulier de 18 côtés Les points sont joints selon le numéro du point multiplié par k et pris modulo 19.
À gauche k = 2 et les points successifs sont: 1, 2, 4, 8, 16, 13, 7, 14, 9, 18, 17, 15, 11, 3, 6, 12, 5, 10, 1. Exemple de calcul: 16 x 2 = 32 et 32 – 19 = 13. Le point qui succède 16 est le point 13. Au milieu k = 3. Essayez avec k supérieur. À droite, k = 8. Formation de trois polygones (colorés).
Brèves associées	>>> Gren		>>> Brèves Énigmes – Index
Pour en savoir plus	>>> Car		>>> P

1068. Deux cercles en arbelos
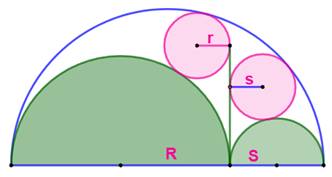
Construction Trois demi-cercles en forme d'arbelos Deux petits cercles tangents à deux demi-cercles et à la perpendiculaire verte. Quelles sont les valeurs des rayons des deux petits cercles (r et s) en fonction des rayons des demi-cercles verts (R et S). Résultat
Brèves associées	>>> Carrés et quatre cercles		>>> Brèves Énigmes – Index
Pour en savoir plus	>>> Deux cercles en arbelos – Démonstration		>>> Sangakus

1069. Constructibilité
Construction à la règle et compas d'un polygone régulier à n côtés Construction impossible Pour les polygones réguliers de 7, 9, 11, 13, 14, 18, 19 … côtés		Construction au compas Théorème de Mohr (1672) ou de Mascheroni (1797): Toute construction à la règle et au compas peut se réaliser au compas seul. Construction à la règle seule Toute construction à la règle et au compas peut être réalisée avec la règle seulement, à condition de diposer d'un cercle. Note: en latin, compar veut dire égal. Le verbe compassare signifiait: mesurer avec ses pas.
Brèves associées	>>> Centre du cercle		>>> Brèves Constructions – Index
Pour en savoir plus	>>> Construction – Index		>>> Polygones réguliers >>> Perpendiculaire sans compas

1070. La maison du maire
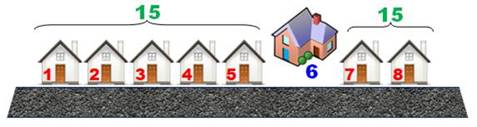
Problème Dans cette rue les numéros des maisons se suivent. La maison du maire a un numéro tel que la somme de tous les autres avant est égale à la somme de tous les autres après. La rue comporte moins de dix maisons.		Illustration Réponse 1 + 2 + 3 + 4 + 5 = 7 + 8 = 15 La maison du maire est au numéro 6
Brèves associées	>>> Le fortin et ses gardes		>>> Brèves Énigmes – Index
Pour en savoir plus	>>> La maison du maire – Explication		>>> Nombre médian de suites équilibrées

1071. Division par 11
Exemple de nombres divisés par 11 (voir le tableau) Le trait de surlignement indique que le nombre visé (la période) est répété sans fin. Ainsi, par exemple, 4/11 = 0,363636… et 7/11 = 0,636363… Division par 11 Pour diviser un nombre par 11, multipliez le numérateur par 9 … Ex: 3/11 => 3 × 9 = 27 => 0,272727… Périodes La division par 11 des nombres de 1 à 10 produit cinq types de suites périodiques à deux chiffres, la période, et leur permutation: {09, 18, 27, 36, 45} Le nombre premier 11 est le plus petit produisant des fractions d'ordre 5. Grand nombres Avec d'autres numérateurs, on retrouve les mêmes décimales précédées d'une partie fixe: 12/11 = 1,090909… 13/11 = 1,181818… 100/11 = 9,090909… 1234/11 = 112,181818…
Brèves associées	>>> Divisibilité par 11	>>> Brèves Opérations – Index
Pour en savoir plus	>>> Division par 11	>>> Nombre 11

1072. Nombre 2520
Nombre divisible par 1 à 10		Méthode Pour trouver le nombre divisible par tous les nombres de 1 à 10 (exemple): Sélectionner chacun des nombres premiers (2, 3, 5 et 7), et Conserver la plus grande puissance de chacun.
Nombre 2520 2 520 = 2^3 × 3^2 × 5 × 7 = 5 × 7 × 8 × 9 = 3 × 4 × 5 × 6 x 7 2 520 = 8! / 4² = 8! / (2 × 2!)² = 8! / 2^4 = 9! / 12² = 9! / (2 × 3!)² = (2+2+2+2)! / (2!×2!×2!×2!)		Propriétés Le plus petit nombre divisible par les nombres de 1 à 10. PPCM des nombres de 1 à 9 et aussi, des nombres de 1 à 10. Super-primorielle de 9 et de 10. Nombre multi pronique Factorielles divisées
Brèves associées	>>> Nombre 2 520		>>> Brèves Nombres – Index
Pour en savoir plus	>>> DicoNombre 2 520		>>> DicoNombre – Index

1073. Forme infinie
Ce type d'égalité se prolonge sans fin. Les deux dernières lignes montrent le principe de formation de chaque égalité. Nombres qui servent à compter les arbres (graphes) étiquetés. Voir OEIS A006963 (planar embedded labeled trees)
Brèves associées	>>> Motif avec retournement	>>> Brèves Motifs – Index
Pour en savoir plus	>>> Pépites de nombres	>>> Motifs avec les nombres

1074. Priorité des opérations
Énigme virale ! Les sites et magazines testent vos capacités de calcul avec ce genre de calcul. Une fois pour toute, apprenez à les résoudre. C'est finalement très simple. Règle de priorité des calculs Dans l'ordre décroissant: parenthèses, divisions et multiplications, et soustractions et additions Aller plus loin Inutile de créer des pièges à nos jeunes étudiants, plaçons des parenthèses partout où il y a risques d'ambigüités. Ceci, d'autant plus que les calculettes standards ne sont pas capables de donner un résultat correct.		Calcul résolu pas à pas Calculatrices et logiciels de calcul Seule la calculatrice en mode scientifique, comme les logiciels, donne le résultat juste. En mode standard, le calcul est linéaire sans mémorisation, donc faux.
Brèves associées	>>> Multiplication avec les doigts		>>> Brèves Calculs – Index
Pour en savoir plus	>>> Priorité des opérations		>>> Calculs – Index

1075. Pythagore généralisé
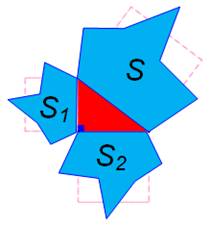
Avec des carrés Vous connaissez le théorème de Pythagore avec des carrés adjacents aux côtés d'un triangle rectangle: a² + b² = c² ou S1 + S2 = S Avec des polygones réguliers Cette relation entre les aires reste valable pour les triangles équilatéraux, comme pour tout polygone régulier. Avec des demi-cercles Cette relation entre les aires reste valable pour les demi-cercles. Avec des formes semblables Cette relation entre les aires reste valable pour trois formes adjacentes aux côtés du triangle rectangle pourvu qu'elles soient semblables (homothétiques).		Dans tous les cas: S = S1 + S2
Brèves associées	>>> Th. de Pythagore – Proportions		>>> Brèves Théorèmes – Index
Pour en savoir plus	>>> Théorème de Pythagore		>>> Similitudes, homothétie

1076. Carré dans le triangle rectangle
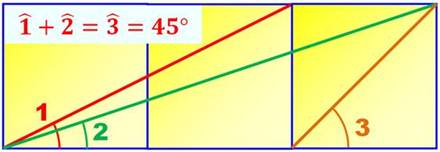
Construction Un triangle rectangle de côtés a, b et c. Un carré bleu adjacent aux deux côtés de l'angle droit et dont un sommet est situé sur l'hypoténuse du triangle. Quelle est la longueur du côté du carré bleu d ? Formule Exemple avec le triangle rectangle (3, 4, 5) d = 3 × 4 / (3 + 4) = 12 / 7 = 1,71428… Itérations Pour les carrés suivants (verts), la formule reste valable en changeant les variables: a prend la valeur d, et b celle de b – d.		Notations Cas du triangle rectangle 3, 4, 5
Brèves associées	>>> Carré maximum dans le triangle rectangle		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Suite de carrés dans le triangle rectangle		>>> Triangle rectangle

1077. Carré dans le triangle rectangle
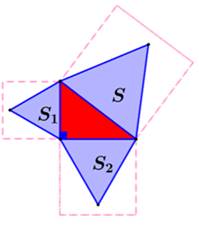
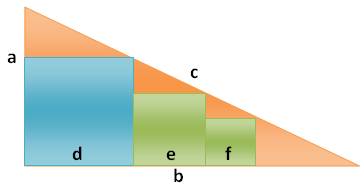
Propriété Trois carrés identiques adjacents l'un à l'autre. L'angle 3 vaut 45° et la somme des deux autres vaut également 45° Piste La démonstration se fait en reproduisant la même bande en haut et en bas de cette bande. Le segment vert est alors la diagonale d'un grand carré.		Propriété amusante avec trois carrés identiques Angle 1 = 26,56° et angle 2 = 18,44°
Brèves associées	>>> Carré divisé – Aire manquante		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Angle de 45° et trois carrés		>>> Passage du bassin

1078. Allumettes
Rétablir l'égalité en déplaçant une seule allumette Solutions des deux jeux		Former trois carrés seulement à partir de cette figure à cinq carrés, en déplaçant trois allumettes.
Brèves associées	>>> Allumettes en carrés		>>> Brèves Jeux – Index
Pour en savoir plus	>>> Jeux avec des allumettes		>>> Allumette en carrés

1079. Triangle – Propriétés
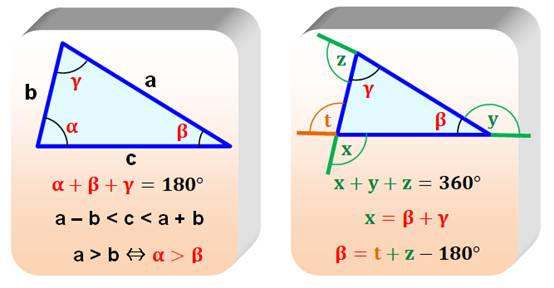
Résumé des propriétés des angles et des côtés des triangles quelconques Partition du triangle quelconque par ses médianes
Brèves associées	>>> Triangle – Partage en six parts égales	>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Triangle quelconque	>>> Résolution des triangles

Retour	Brèves de maths – Page 53
Suite	Brèves de maths – Page 55
Voir	Voir liens en haut de page
Cette page	http://villemin.gerard.free.fr/NombDico/aBreves/Breve54.htm

Solution des énigmes avec des allumettes

Rétablir l'égalité en déplaçant une seule allumette

Former trois carrés

Retour