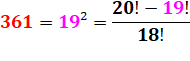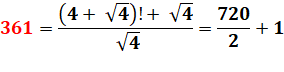|
Édition du: 01/02/2023 |
![]()
|
|
Nouvelle
orthographe avec
des traits d'union partout |
||||||||
|
|
![]()
Chiffres et numération
|
361 – (3 + 6 + 1) = 351
= T26 361 – (3 × 6 × 1) = 343 |
|
|
361 = 19² & 3 +
1 = 4 = 2² |
|
|
361 |
|
|
361, [4, 19],
[3c, 16], [8c, 10], [10c, 9], [24c, 6], [36c, 5], [60c, 4], [120c, 3] |
|
|
361 = 19²
36 = 6² et 1 = 1² |
|
|
361 = 19² 3 + 6 + 1 = 1 + 9 = 10 |
|
Addition et
soustraction
|
361 =
10 + 11 + … + 28 |
|
|
|
|
|
361 = T14 +
T15 + T16 = T18 + T19 |
|
Multiplication et division
|
361 = (3²x6²x1²) +
(4+7+0+4+5+8+8+1) Avec
3613 = 47 045 881 |
|
|
361, 25, [867, 935, 2299, 2471, 3839, 4511, 7751,
9599, 13631, 14711, 16271, 19631, 22199, 22991, 24119, 25511, 26471, 27359,
29591, 29999, 30551, 31439, 32111, 32231, 32399] |
|
|
361 = (6! + 2! ) / 2! = 1 + 3 x 4 x 5 x 6 |
Avec les
puissances
|
361 = 19²
= 1² + 6² + 18²
= 6² + 6² + 17²
= 6² + 10² + 15² |
|
|
361 = 19² = 1 + 3 + 5 +
… + 37 |
|
En
puissances
|
2361 = 4697 …76664…9952 = 1,7… 10162 |
|
Autour du nombre
|
361, 529, 784 |
|
|
361,9986…
|
|
Jeux
|
|
|
![]()
|
|
Voir Diviseurs, Quantité,
Somme,
Fonctions
arithmétiques
|
Numération: base, [chiffres] |
Repdigit (Brésilien) |
||
|
2,
[1, 0, 1, 1, 0, 1, 0, 0, 1] 3,
[1, 1, 1, 1, 0, 1] 4,
[1, 1, 2, 2, 1] 5,
[2, 4, 2, 1] 6,
[1, 4, 0, 1] 7, [1, 0, 2, 4] 8,
[5, 5, 1] 9,
[4, 4, 1] 10,
[3, 6, 1] 11,
[2, 10, 9] |
12,
[2, 6, 1] 13,
[2, 1, 10] 14,
[1, 11, 11] 15, [1, 9, 1] 16,
[1, 6, 9] 17,
[1, 4, 4] 18, [1, 2, 1] 19, [1, 0, 0] 20,
[18, 1] 21,
[17, 4] |
22,
[16, 9] 23,
[15, 16] 24,
[15, 1] 25,
[14, 11] 26,
[13, 23] 27,
[13, 10] 28,
[12, 25] 29,
[12, 13] 30,
[12, 1] 60,
[6, 1] |
360,
[1, 1] |
Voir Bases
/ Brésiliens
![]()
|
Retour Suite |
|
|
Voir |
|
|
Voir |
![]()