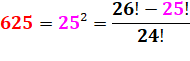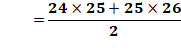Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 05/07/2023 M'écrire Brèves de Maths

DicoNombre Débutant Glossaire Types de nombres Nom des nombres Écriture des nombres Table des facteurs Langues	Dictionnaire des Nombres
	0 / 1 / 10 / 100 / 200 / 300 / 400 / 500			600 à 699			700 / 800 / 900 / 1 000 / 2 000 / 5 000 / 10 000 / 100 000 / 10^6 / 10^9 / 10^100
	600	610	620	630	640		650	660	670	680	690
	620	621	622	623	624	625		626	627	628	629

Six-cent-vingt-cinq.

Six hundred twenty five

Orthographe / Langues

Facteurs
Binaire	10 0111 0001
Octal Hexa	1161 271
Romain	DCXXV

Suite

Automorphe (5^e)

Composé

Déficient

Docile (amenable)

Friedman

Frugal

Interpremier

NRC

Refactorisable ou tau

Trimorphe

Géométrique

Carré

Octogonal centré

Friedman 625 = 5^6 – 2

Automorphes 625 = 25² 625² = 390 625

625 = 5^4 = 25² = 7² + 24² = 19 + 576 = 15² + 20² = 225 + 400		Nombre n à la puissance n-1. Carrés et somme de carrés. Solution de a² + b² = z^4.
…5^4 = …0625 15^4 = 50 625 95^4 = 81 450 625 625^4 = 152 587 890 625		Un nombre terminé par 5 à la puissance 4 se termine par 0625.
0,…625 = 2^-2k125 = (2^-2k x 10^2k) mod 1000		Toutes les puissances négatives de 2 d'ordre pair se terminent par 625, les autres par 125.
625 – 526 = 99 625 – (5x2x6) = 565	Devient repdigit en lui retirant son retourné et palindrome en lui retirant le produit de ses chiffres
625 = 5^6 – 2	Anagrammes numériques. Nombre de Friedman.
	Carré = cette relation entre factorielles successives.
		Jeu du quatre 4. Avec la notation anglaise: .4 = 0,4 = 2/5

625 = 13 + 14 + … + 37	Une des quatre sommes de nombres consécutifs >>>
	Somme de deux nombres triangulaires consécutifs.
625 = 73 + 79 + 83 + 89 + 97 + 101 + 103	Sommes de sept premiers consécutifs. Nombre octogonal centré.
625 = 7² + 24² = 15² + 20²	Deux seules sommes de deux carrés >>>
	Carré + puissance = puissance.
625 = 5^4 256 = 4^4	Motif avec permutation des chiffres. Ici, avec puissance quatrième de nombre consécutifs.
= 5^4 = 2^4 + 2^4 + 3^4 + 4^4 + 4^4	La plus petite puissance 4^e égale à la somme de 5 puissances 4^e.
625 = 5^6 – 2	Mêmes chiffres de part et d'autre de l'égalité: nombre de Friedman.
625 = 25² = 1 + 3 + 5 +…+ 49	Le carré de n est la somme des n premiers impairs.
625 = 164 + 641 = 25² = 263 + 362	Nombre NRC: nombre + retourné = carré

625 x 625 = 390 625 625 x 762 = 476 250 625 x 5 625 = 3 515 625	Produits qui contiennent leurs opérandes. La deuxième est la plus grande pour toutes les multiplications jusqu'à 1000 x 1000.
625^2 = 390625 625^3 = 244140625 625^k = … 625 Voir Nombre 50 625	Nombre plaqué carré ou automorphique. Seul nombre à trois chiffres avec 376 qui, en ajoutant un nombre à gauche, donne son carré (25 et 76 pour deux chiffres). Nombre plaqué cube ou trimorphique Toutes les puissances des nombres en …625 se terminent en 625. Rare motif en n² – n = 0 mod 1000.
625^2 + 1 250² = 125^3 625^3 + 1 250^3 = 46 875²	Couples de nombres dont la somme des carrés est un cube et celle des cubes et un carré Formule générique: A = 625 M^6 et B= 2A Exemple avec M = 3: A = 455 625 et B = 911 250 A² + B² = 10 125² et A^3 + B^3 = 922 640 625^2
	Toutes ces puissances de 2 se terminent de plus en plus par les mêmes chiffres. De même pour la puissance de 5 et le produit indiqué. Voir Nombre 376 / Nombre 432 Voir Nombres p-adiques

Identité détaillée

Voir Diviseurs, Quantité, Somme, Fonctions arithmétiques

Numération: base, [chiffres]			Repdigit (Brésilien)
625 2, [1, 0, 0, 1, 1, 1, 0, 0, 0, 1] 3, [2, 1, 2, 0, 1, 1] 4, [2, 1, 3, 0, 1] 5, [1, 0, 0, 0, 0] 6, [2, 5, 2, 1] 7, [1, 5, 5, 2] 8, [1, 1, 6, 1] 9, [7, 6, 4] 10, [6, 2, 5] 11, [5, 1, 9]	12, [4, 4, 1] 13, [3, 9, 1] 14, [3, 2, 9] 15, [2, 11, 10] 16, [2, 7, 1] 17, [2, 2, 13] 18, [1, 16, 13] 19, [1, 13, 17] 20, [1, 11, 5] 21, [1, 8, 16]	22, [1, 6, 9] 23, [1, 4, 4] 24, [1, 2, 1] 25, [1, 0, 0] 26, [24, 1] 27, [23, 4] 28, [22, 9] 29, [21, 16] 30, [20, 25] 60, [10, 25]	124, [5, 5] 624, [1, 1]

Voir Bases / Brésiliens

Suite	Voir Haut de page / Autres nombres
Voir	Nombres par leur nom Empreinte des nombres DicoNombre Junior Historique de ce site et Références Maitres en nombres
Cette page	http://villemin.gerard.free.fr/NombDico/N5002000/aaaN600/N625.htm