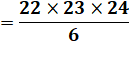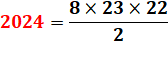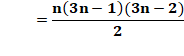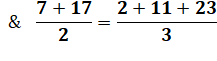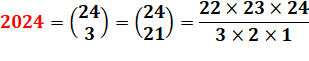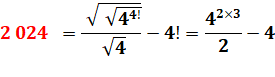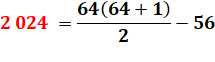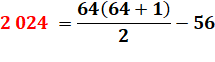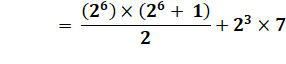|
Édition du: 14/02/2025 |
|
Dictionnaire des Nombres |
|||
|
1 / 10 / 50 / 100 / 500
/ 1000 / 1500 / 1900 / 2000 / 2016 / 2017 / 2018
/ 2019 / |
2024 |
2031 à
2099 / 3000 / 5000 / 10 000 / 20 000 / 50 000 / 100 000 / 106 / 109
/ 10100 Autres |
|
|
2020 / 2021 / 2022
/ 2023 / 2024 / 2025 / 2026 / 2027 / 2028
/ 2029 / 2030 |
|||
|
Humour
2023-2024 |
||
|
Chiffres de
2024 (jeu) |
Faites
un double-clic pour un retour en haut de
page
![]()
Carte d'identité du nombre
|
2,024 103 |
|
|||||||||||||||
Suite en propriétés
arithmétiques Voir
Année 2023 |
Voir Nom des nombres
|
|||||||||||||||
Chiffres
et Numération
|
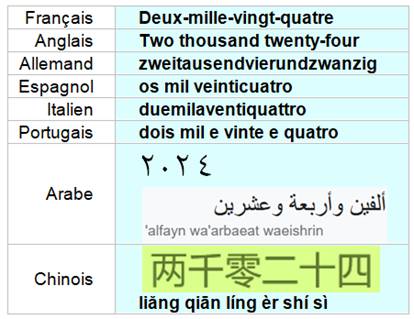
2024 |
|
|
|
2024 =
210 + 0 + 210 – 4! |
|
|
|
2024 =
11×2×2×2×23 ➪ 1122223 |
|
|
|
|
|
|
|
2024 +
4202 = 6226 |
|
|
|
202 × 4 =
808 |
|
|
|
20 × 24
=
16 20 + 24
=
17 |
Propriété valable pour
tous les nombres à quatre chiffres ayant un 0 comme chiffre des centaines. |
|
|
2 02410 = 22022223 |
|
|
|
2 024 = 44 × 45
+ 44 |
Notez les deux nombres
successifs 44 et 45.
|
|
2 024 = 1000 + 211 – 210 |
|
|
2 024 = 77 + 78 + … + 99 =
119 + 120 + … + 134 =
179 + 180 + … + 189 |
|
|
2 024 = T1 + T2 + … + T22
|
|
|
|
|
|
2024 = 179 + 180 + …
+ 189 |
|
Multiplication,
division
|
2024
= 2
× 1012 = 22 × 92 |
Les six produits de deux nombres
égaux à 2024: 2 × 1012; 4 ×
506; 8 × 253; 11 ×
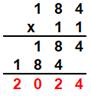
184; 22 × 92; 23 ×
88; 44 × 46. |
|
|
2024
= 23 × 253 |
|
|
|
2023
= 7 × 17² 2024
= 22 × 506 2025
= 34 × 5² |
|
|
|
2024
= 11 × 184 |
|
|
|
2024 =
22 × 23 × 24 / 6 |
Un nombre premier est de la forme
6n±1. Alors, l'un des deux nombres est de la forme 6n et le produit est
divisible par 6. |
|
|
{11,
22, 44, 88} | 2024 |
|
|
|
2024
= 23 × 253 2025
= 33 × 75 |
|
|
|
|
Les diviseurs
propres de l'un moins 1 est égal à l'autre. |
|
|
|
|
|
|
2024 =
i × (1 + i)6 × 11 × 23 |
|
|
|
2 023 = 7 × 17² 2 024 = 2² × 506 2 025 = 5² × 81 |
|
|
2 023 = 7 × 17² 2 024 = 23 × 11 × 23
|
Deuxième
cas après 459. |
|
2 022 / (2+0+2+2) = 337 2 023 / (2+0+2+3) = 289 2 024 / (2+0+2+4) = 253 2 025 / (2+0+2+5) = 225 |
Liste des têtes de série: 510, 1014, 2022, 3030, 10 307, 12 102, 12 255, 13 110, … |
|
2 023 = 17² × 7 2 024 = 23 × 253 2 025 = 34 × 25 |
Liste: 350, 1375, 2023, 11150, 11374, 12446, 13310, |
Avec
les puissances
|
2 024 = 322 + 103 = 412
+ 73 |
|
|
|
2 024 = 45 + 103 |
|
|
|
2024
= 2025 – 1 = 45² – 1 = (45 – 1)(45 + 1) = 44 × 46 |
Conduit à une factorisation par deux
nombres pairs successifs. De la forme: n(n+2) = (n+1)² – 1. |
|
|
2 024 = 2² + 4² + 6² + … + 22² |
|
|
|
2024
= 46² – 2 × 46 |
|
|
|
2024
= 22 + 162 + 422 … 2024 =
18² + 20² + 20² + 30² |
|
|
|
2024
= 22 + 4² + … + 22²
=
2n (n+1) (2n+1) / 3 |
|
|
|
2024 =
83 + 83 + 103 |
|
|
|
2024 =
23 + 23 + 23 + 103 + 103 = 23 + 23 + 43
+ 63 + 123 = 33 + 33 + 83
+ 93 + 93 |
Jamais somme de jusqu'à huit
puissances supérieures à 3. |
|
|
2024
= 23 + 33 + … + 93 … 2024
= 7 × 63 + 83 |
24 fois somme de jusqu'à huit cubes
dont ces deux exemples. Les chiffres de l'exemple forment le
nombre 23 456 789 qui est le plus
grand nombre premier avec chiffres strictement croissant. |
|
|
2024
= 23 + 33 + … + 93 =
(1+2+3+4+5+6+7+8+9)² – 1 |
|
|
|
2024 =
211 – 4! = 2048 –
24 |
|
|
|
2024 =
210 + 103 |
|
|
En
puissance
|
|
|
|
2024² = 4 096 576 4096 = 64² 576 = 24² |
|
|
22024 = 1926 …36660…7216 = 1,9… 10609 |
|
|
|
|
Dénombrement, jeux et curiosités
|
|
|
|||||
|
2 024 = 12 × 23 × 11 × 13 |
|
|||||
|
2 024 = 1234 – 5 + 6 + 789 = 123 + 4(5 + 6 x 78) + 9 = 9 × 8 + 7 + 6 × 54 × 3 × 2 + 1 |
|
|||||
|
2 024 = 2222 – 222 + 22 + 2 |
|
|||||
|
|
|
|||||
|
|
Factorielle
4 = 1×2×3×4 et la double racine supprime l'effet du
facteur 4. Sinon
44! = 281 474 976 710 656. |
|||||
|
|
Voir
la suite dite du commentaire
numérique |
|||||
|
|
Merci à Claude
Renouf |
|||||
|
2 024 |
|
|||||
|
2 024 |
|
|||||
|
|
|
Exemple
|
![]()
|
·
2024 est une année
bissextile. Année qui commence un lundi. 52 dimanches. 2 vendredis 13: 13 septembre et 13 décembre. La 2024e
année de notre ère, La 24e
année du IIIe millénaire et du XXIe siècle, et La 5e
année de la décennie 2020-2029. Élections
européennes en juin. Jeux
Olympiques à Paris en juillet-août, et septembre pour les paralympiques. Élections
présidentielles aux États-Unis en novembre. |
||
|
·
Le
nombre 2024 est présent 488 fois dans
l'encyclopédie des suites OEIS. |
|
|
Voir Diviseurs, Quantité, Somme, Fonctions arithmétiques
|
Numération: base, [chiffres] |
Repdigit (Brésilien) |
||
|
2,
[1, 1, 1, 1, 1, 1, 0, 1, 0, 0, 0] 3, [2, 2, 0, 2, 2, 2, 2] 4,
[1, 3, 3, 2, 2, 0] 5,
[3, 1, 0, 4, 4] 6, [1, 3, 2, 1, 2] 7,
[5, 6, 2, 1] 8,
[3, 7, 5, 0] 9,
[2, 6, 8, 8] 10,
[2, 0, 2, 4] 11,
[1, 5, 8, 0] |
12,
[1, 2, 0, 8] 13,
[11, 12, 9] 14,
[10, 4, 8] 15,
[8, 14, 14] 16,
[7, 14, 8] 17,
[7, 0, 1] 18, [6, 4, 8] 19,
[5, 11, 10] 20,
[5, 1, 4] 21, [4, 12, 8] |
22,
[4, 4, 0] 23,
[3, 19, 0] 24,
[3, 12, 8] 25,
[3, 5, 24] 26,
[2, 25, 22] 27,
[2, 20, 26] 28,
[2, 16, 8] 29,
[2, 11, 23] 30,
[2, 7, 14] 60,
[33, 44] |
45, [44, 44] 87,
[23, 23] 91,
[22, 22] 183,
[11, 11] 252,
[8, 8] 505,
[4, 4] 1011,
[2, 2] 2023,
[1, 1] |
Voir Bases / Brésiliens
|
Valeur en base 10 de 2023 en base b Exemple:
20233 => 2×33+0×32+2×31+3×30=
6310 |
|||
|
2,
24 3,
64 4,
140 5,
264 |
6,
448 7,
704 8,
1044 9,
1480 |
10,
2024 11,
2688 12,
3484 13,
4424 |
14,
5520 15,
6784 16,
8228 |
Haut de page (ou double-clic)
![]()
|
Retour |
|
|
Suite |
|
|
Sites |
|
|
Cette page |
![]()