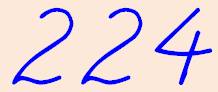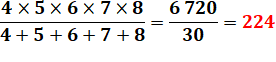Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 06/07/2023 M'écrire Brèves de Maths

Débutant Glossaire Types de nombres Nom des nombres Écriture des nombres Table des facteurs Langues	Dictionnaire des Nombres
	0 / 0,… / 1 / 10 / 50 / 100		200 à 300		300 / 400 / 500 / 600 / 700 / 800 / 900 / 1 000 / 2 000 / 5 000 / 10 000 / 100 000 / 10^6 / 10^9 / 10^100
	200	210	220	230	240	250	260	270	280	290
	220	221	222	223	224	225	226	227	228	229

Faites un double-clic pour un retour en haut de page

Deux-cent-vingt-quatre

Two hundred twenty four

Nouvelle orthographe

avec des traits d'union partout

Facteurs
Binaire	1110 0000
Bases	220223 EE15 8827
Romain	CCXXIV

Suite en propriétés arithmétiques

Abondant

Admirable

Binomial (même puissance)

Congruent

Composé

Cunningham

Docile (amenable)

Élégant

Granville (ou S-parfait)

Harshad

Harshad SP

Pair

Pratique

Semi-parfait

S-parfait

Zuckerman

Zumkeller

Chiffres et numération

182 = 224 cent-quatre-vingt-deux = deux-cent-vingt-quatre	Anagramme numérique. Jean-Charles Meyrignac
224 + 422 = 646	Devient palindrome en lui ajoutant son retourné.
224 / (2 + 2 + 4) = 28 224 / (2 x 2 x 4) = 14	Nombre de Harshad SP: divisible à la fois par la somme et le produit de ses chiffres. Aussi divisible par chacun de ses chiffres.

Addition et soustraction

224 = 35 + 34 +…+ 29 = 28 x 8

Somme de consécutifs, égale à un multiple du précédent. >>>

Multiplication et division

224 = 2^5 x 7		Nombre divisible par 32 = 2^5.
224 = 3 x 5 x 15 – 1 = 2 x { (3–1) (5–1) (15–1) }		Deux solutions seulement (2, 4, 8) et (3, 5, 15) pour (a – 1) (b – 1) (c – 1) (abc – 1) Rappel: la barre verticale veut dire divise
		Motif avec factorielle tronquée.
1+ 2 + 3 + … + 224 = 25 200 = 35 x 6! = 5 x 7!	La somme des nombres de 1 à 224 est divisible par 6! = 720 et par 7! = 5 040. Avec la somme des nombres jusqu'à n: S = n (n + 1) / 2:
Moyenne des diviseurs = 42	Un nombre entier.
224 = tau (665 280)	Quantité de diviseurs de 665 280, nombre hautement composé.

Avec les puissances

224 = 2^8 – 2^5	Différence de puissances d'un même nombre.
224 = 4² + 8² + 12² = (1² + 2² + 3²) 4²	Somme de carrés. Le plus grand nombre non-somme de cinq carrés distincts. Voir Nombre 225
224 = 2^3 + 6^3 = 2^3 + 3^3 + 4^3 + 5^3 = 14 x 16 = 15² – 1² = 18² – 10² = 30² – 26² = 57² – 55²	Nombre binomial. Somme de quatre cubes toujours divisible par 2(2n+3). Voir Autour de 12345
224 = 2^5 + 2^7 + 4^3	Nombre élégant: somme de ses chiffres en puissance.

En puissance

2^224 = 26959946667…14442…49216 = 2,6… 10^67

Nombre apocalyptique.

Jeux

Jeu du quatre 4. Avec la notation .4 qui vaut 2/5 = 0,4

Identité détaillée

Voir Diviseurs, Quantité, Somme, Fonctions arithmétiques

Numération: base, [chiffres]			Repdigit (Brésilien)
2, [1, 1, 1, 0, 0, 0, 0, 0] 3, [2, 2, 0, 2, 2] 4, [3, 2, 0, 0] 5, [1, 3, 4, 4] 6, [1, 0, 1, 2] 7, [4, 4, 0] 8, [3, 4, 0] 9, [2, 6, 8] 10, [2, 2, 4] 11, [1, 9, 4]	12, [1, 6, 8] 13, [1, 4, 3] 14, [1, 2, 0] 15, [14, 14] 16, [14, 0] 17, [13, 3] 18, [12, 8] 19, [11, 15] 20, [11, 4] 21, [10, 14]	22, [10, 4] 23, [9, 17] 24, [9, 8] 25, [8, 24] 26, [8, 16] 27, [8, 8] 28, [8, 0] 29, [7, 21] 30, [7, 14] 60, [3, 44]	15, [14, 14] 27, [8, 8] 31, [7, 7] 55, [4, 4] 111, [2, 2] 223, [1, 1]

Voir Bases / Brésiliens

Retour Suite	Nombre 223 Nombre 225
Voir	Nom des nombres Nombres géométriques
Voir	Nombres par leur nom Empreinte des nombres DicoNombre Junior Historique de ce site et Références Maitres en nombres

Cette page

http://villemin.gerard.free.fr/NombDico/N100a500/Nomb200/Nb224.htm