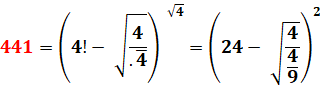|
Édition du: 12/03/2024 |
![]()
|
|
Nouvelle
orthographe avec
des traits d'union partout |
||||||||
|
|
![]()
Chiffres et numération
|
44110 = 14419 |
|
|
441 =
21² et 4 = 2², 4 = 2², 1 = 1² 144
= 12² |
|
|
441 x 144 = 252² |
|
|
441 + 144 = 585 441 × (4×4×1) = 7056 = 84² |
|
Addition
et soustraction
|
441 = 11 + 12 + … + 31 |
|
|
|
441 = T20 +
T21 = n² + 2n + 1 pour n = 20 |
|
|
Multiplication, division, diviseurs
|
|
|
Avec les
puissances
|
441 = 21² = ( 1 + 2 + 3 + 4 + 5 + 6) ² = 13 + 23
+ 33
+ 43 + 53
+ 63 = 29² –
20² = 35² –
28² =
75² – 72² = 221² –
220² |
Voir Autour de 12345 |
|
441 = 21² = 3²
x 7² = 7² + 4x7² + 4x7²
= 7² + 14² + 14²
= 4² + 5² + 20²
= 4² + 8² + 19²
= 4² + 13² + 16²
= 6² + 9² + 18²
= 8² + 11² + 16² |
|
|
441 = 29² – 20² = 21² =
7² x 3² |
|
|
441 = 13 + 23 + 33 + 43
+ 53 + 63 = 21 x 21 |
|
|
441 = 21² = 1 + 3 + 5
+ … + 29 + 31 + 33 + … + 41
= 192 + 63 |
|
|
441 = 13 +
23 + 33 + 43 + 53 + 63
= 63 x 7 |
|
|
441 = 21² = 13
+ 23 + 63 + 63 |
Rappel 33 + 43
+ 53 = 63 |
En puissance
|
|
Dénombrement, jeux et curiosités
|
|
|
||
|
|
Avec
la notation anglaise: |
||
|
441 |
|
||
![]()
|
|
Voir Diviseurs, Quantité,
Somme,
Fonctions
arithmétiques
|
Numération: base, [chiffres] |
Repdigit (Brésilien) |
||
|
2,
[1, 1, 0, 1, 1, 1, 0, 0, 1] 3,
[1, 2, 1, 1, 0, 0] 4, [1, 2, 3, 2, 1] 5,
[3, 2, 3, 1] 6,
[2, 0, 1, 3] 7,
[1, 2, 0, 0] 8,
[6, 7, 1] 9,
[5, 4, 0] 10,
[4, 4, 1] 11,
[3, 7, 1] |
12,
[3, 0, 9] 13,
[2, 7, 12] 14,
[2, 3, 7] 15,
[1, 14, 6] 16,
[1, 11, 9] 17,
[1, 8, 16] 18,
[1, 6, 9] 19,
[1, 4, 4] 20, [1, 2, 1] 21,
[1, 0, 0] |
22,
[20, 1] 23,
[19, 4] 24,
[18, 9] 25,
[17, 16] 26,
[16, 25] 27,
[16, 9] 28,
[15, 21] 29,
[15, 6] 30,
[14, 21] 60,
[7, 21] |
48,
[9, 9] 62,
[7, 7] 146,
[3, 3] 440,
[1, 1] |
Voir Bases
/ Brésiliens
![]()
|
Retour Suite |
|
|
Voir |
|
|
Voir |
![]()