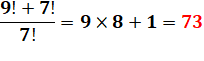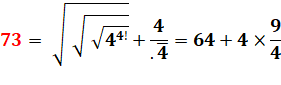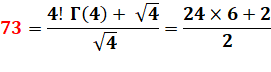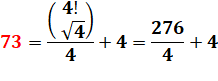|
Édition du: 03/05/2025 |
|
Dictionnaire des Nombres |
||||||||||||
|
100 / 200 |
||||||||||||
![]()
|
|
Nouvelle
orthographe avec
des traits d'union partout |
|||
|
|
Devient deux lettres par rotation de
180° |
|||
|
Caractérisation
du nombre
|
|
Voir |
||
|
Quels
sont les trois nombres tels que, en ajoutant 73 à chacun, le premier vaut le
double de la somme des autres, le deuxième le triple et quatrième le
quadruple ? |
|
|
||||
|
SAVOIE |
||||
|
73 = 1 x 73 |
TANTALE
Ta |
|||
|
Propriétés Typiques |
73 x 137 = 10
001 |
CAME |
||
|
|
|
|||
|
|
||||||
|
|
Voir Numération 70 à 79 |
|||||
|
|
||
|
Codage |
|
|
|
Transport |
||
|
Revolver
français mis en production en 1973 à Mulhouse. Développé pour la police et de
la gendarmerie, notamment pour leurs unités spéciales. |
|
|
|
est
compté indépendamment du livre de Jérémy. |
Chiffres et numération
|
7310 = 3722 |
|
|
2, 3, 5, 7, 11, 13, 17, 23, 31, 37, 41, 43, 47, 53, 71, 73 |
|
|
73
= 37 × 2 – 1 |
Suivants:
251 = 2 x 125 + 1; 2519 = 2 x 1259 + 1 |
|
73 × 37 = 2701 = T73 73 – 37 = 36 = T8 |
|
|
73 = 1 x 73 |
En notant que 21 = 7 x 3. |
|
73 = 37 × 2 – 1 793 = 397 × 2 – 1 7993 = 3997 × 2 – 1 … |
Seul cas
pour k = 2 et h = -1, mais nombreuses familles pour d'autres valeurs de k et
h. |
|
37
& 73 sont
premiers 12e & 21e premiers |
C'est le plus
grand nombre tel que toutes les combinaisons de ses chiffres sont
premiers. |
Anecdote
|
Les
fans de la série The Big Bang Theory
se souviennent peut-être que le Dr Sheldon Cooper a dit: Le
meilleur nombre est 73. Pourquoi ? 73 est le 21e nombre premier.
Son miroir, 37, est de 12e
et son miroir, 21, est le produit de la multiplication de 7 x 3. En
binaire 73 est un palindrome, 1001001, qui à l'envers est 1001001. |
Rapporté de
nombreuses fois par la presse des années 2020
|
73 = 111 8
= 1001001 2 |
|
||
|
73 = 6 x 4 (4 – 1) + 1 |
Voir
dames chinoises |
||
|
73 nombres
composés 25 nombres
premiers 1 nombre spécial
le 1. |
|
||
|
73 = 73
1 facteur 74 = 2 x 37
2 facteurs 75 = 3 x 5²
3 facteurs |
|
||
|
73 = 37 x 2 – 1 793 = 397 x 2 – 1 7993 = 3997 x 2 – 1 …. |
|
||
|
73, 115, 82, 9232 Cycle: 73, 220,
110, 55, 166, 83, 250, 125, 376, 188, 94, 47, 142, 71, 214, 107, 322, 161,
484, 242, 121, 364, 182, 91, 274, 137, 412, 206, 103, 310, 155, 466, 233,
700, … |
|
||
|
73 |
|
||
Multiplication, division, diviseurs
|
|
La somme alternée
des blocs de quatre chiffres doit être divisible par 73. |
|
73 = 37 x 2 – 1 |
N = 2n -1 ou 2n ou 2n +1 Ce motif se répète en ajoutant des 9
au centre du nombre. |
|
73 x 13 837 = 1 010
101 73 x 13 837 x 37 = 37373737 |
|
|
73 = 365 / 5 |
|
|
|
|
|
10 001 , 137 & 73 |
|
|
73 [98, 175, 335, 671, 767, 1007, 1247, 1271] |
Le nombre
73 est la somme des diviseurs propres de ces 8 nombres (somme aliquote). Plus
petite valeur pour huit sommes. |
Les divisions par 73 sont périodiques d'ordre 9
|
La division par 73 des nombres de 1 à 72 produit neuf types
de suites périodiques à huit chiffres et leur permutation. Le nombre premier 73
est le plus petit produisant des fractions d'ordre 9. Avec d'autres numérateurs, on retrouve les mêmes décimales,
éventuellement en permutation
circulaire, précédées d'une partie fixe: 100/73 =
1,36986301 369… |
|
Avec les puissances
|
73 = 37² – 36² = 37 +
36 |
|
|
|
73
= 9² – 9 + 1 |
|
|
|
73 |
|
|
|
73 = 3² + 8² =
1² + 6² + 6² =
4² + 4² + 4² + 5² = 13 + 23 + 43 |
Notez la somme de trois cubes différents: le nombre 73 est le plus
petit nombre premier somme de trois cubes différents. |
|
|
73 = 3² + 1x8² = 1² + 2x6² = 5² + 3x4² = 3² + 4x4² = 7² + 6x2² = 1² + 8x3² = 8² + 9x1² |
|
|
|
73 = 80 +
81 + 82 = 1118 |
|
|
|
73 = 1 + 36 + 36 = 1!²
+ 3!² + 3!² 73 = 1337 |
|
|
|
73 => x6
+ … + z6 |
Voir Théorème
de Waring |
|
En puissance
|
73² = 5 329 |
|
|
|
73² = 48² + 55² = 2304 + 3025 = 5329 |
|
|
|
739
= 58871586708267913
=> 5+8+8+…+3 = 91 9110
= 38941611811810745401
=> 3+8+9+…+1 = 73 |
|
|
|
7310 = 4297625829703557649 et Sch = 100 |
|
|
Autour du nombre
|
= 447011 5461512684 3408912571 3812505111 0076800700 2829050158 1908009237
0422104067 1833170169 0368000000 0000000001 |
|
Jeux et curiosités
|
|
|
|
73 + 21 = 94 37 + 12 = 49 |
|
|
73 x 375 = 27 375 |
Jeu du quatre 4
|
|
Emploi de racines emboitées et de .4
surligné qui vaut 0,444… = 4/9 |
|
|
|
|
|
|
|
|
|
|
73
= 4 x 4 x 4 + 4 + 5 |
|
|
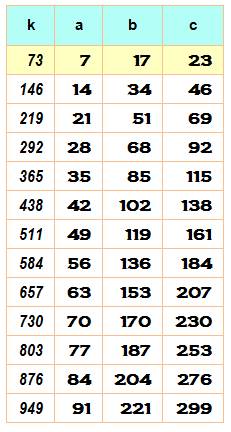
Question Quels sont les trois nombres tels que, en ajoutant 73 à
chacun, le premier vaut le double de la somme des autres, le deuxième le
triple et quatrième le quadruple? Solution La solution est donnée par le système
d'équations, avec k
= 73:
Dont les racines sont: a = 7, b = 17 et c = 23. Autres solutions avec k Faisons varier k, alors k = 73 est la plus petite
solution. Le tableau de droite donne les 13 possibilités jusqu'à 1000. Il y
en a 136 jusqu'à 10 000. Autres solutions avec les coefficients multiplicateurs Avec les coefficients (3, 4, 5), la première solution
est: k = 83. Le tableau de droite donne les
premières valeurs suivantes. La colonne coef indique le premier coefficient
c, et les autres sont c+1 et c+2. |
|
|
|
Voir Diviseurs, Quantité,
Somme,
Fonctions
arithmétiques
|
Numération: base, [chiffres] |
Repdigit (Brésilien) |
||
|
2, [1, 0, 0, 1, 0, 0, 1] 3,
[2, 2, 0, 1] 4,
[1, 0, 2, 1] 5, [2, 4, 3] 6,
[2, 0, 1] 7,
[1, 3, 3] 8, [1, 1, 1] 9,
[8, 1] 10,
[7, 3] 11,
[6, 7] |
12,
[6, 1] 13,
[5, 8] 14,
[5, 3] 15,
[4, 13] 16,
[4, 9] 17,
[4, 5] 18,
[4, 1] 19,
[3, 16] 20,
[3, 13] 21,
[3, 10] |
22,
[3, 7] 23,
[3, 4] 24,
[3, 1] 25,
[2, 23] 26,
[2, 21] 27,
[2, 19] 28,
[2, 17] 29,
[2, 15] 30,
[2, 13] 60,
[1, 13] |
8,
[1, 1, 1] 72,
[1, 1] |
Voir Bases
/ Brésiliens
![]()
|
Suite |
|
|
Cette page |
![]()