Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 16/02/2024 M'écrire Brèves de Maths

DicoNombre Débutant Glossaire Types de nombres Nombres géométriques Nom des nombres Écriture des nombres Table des facteurs Nombres et anglais Langues	Dictionnaire des Nombres
	1 / 10 / 50 / 60 / 70 / 75 / 80 / 85 / / 86 / 87 / 88 / 89 / 90 / 91 / 92 / 93 / 94 / 95 / 96 / 97 / 98 / 99 / 100 / 101 / 102 / 103 / 104 / 105 / 106 / 107 / 108	109	110 / 111 / 112 / 113 / 114 / 115 / 116 / 117 / 118 / 119 / 120 / 125 / 130 / 140 / 150 / 200 / 250 / 300 / 400 / 500 / 1000 / Autres

Transfusion = 109 ou Transfusion 209

Voir Pensées & humour / Cent, sang … / Alphabet parlant / Cent en 9

Cent-neuf

One hundred (and) nine

Orthographe / Langues

Facteurs
Diviseurs	1, 109
Quantité	2
Somme	110
Binaire	110 1101
Romain	CIX

Suite en propriétés arithmétiques

Congruent

Déficient

Docile (amenable)

Heureux

Impair

Jonction

Jumeau avec 107

Premier (29^e)

Premier cubain

Premier de Chen

Premier de Pierpont

Premier de Pythagore

Premier faible

Premier long

Premier régulier

Géométrique

Triangulaire centré (9^e)

18 gonal centré

Stobogrammatique

Chimie	N° 109 = Meitnerium, découvert en 1982.	>>>
Cosmologie	109 : quantité d'astéroïdes vagabonds potentiellement dangereux pour la Terre. 109^e astéroïde 1997 XF11. Découvert en décembre 1997 avec le télescope de Kitt Peak (Arizona), dédié à la veille des astéroïdes dans le cadre du Spacewatch Program.	Astéroïdes et comètes
Géométrie	109° 28' & 70° 32' Angles du losange situé au fond des alvéoles des ruches d'abeilles. Calculés en 1712 par Maraldi (Fr); Confirmé par Mac Laurin (GB).	>>>
Chimie	L’angle entre deux liaisons C-H du méthane est de 109,28°.	>>>

Chiffres et numération

109 – (1+0+9) = 99	Devient palindrome en lui retirant la somme de ses chiffres.
	Mêmes chiffres de part et d'autre de l'égalité.
109 x 9 = 981	Nombre dont un multiple inverse ses chiffres en tête et en queue. Autres à trois chiffres: 208 et 218.

Addition et soustraction

109 = T7 + T8 + T9 = 3/2 n(n+1) + 1 = ½ (3 x 8² + 3 x 8 + 2)	Somme de nombres triangulaires consécutifs. Nombre triangulaire centré.
109 = 31 + 37 + 41	Somme de premiers consécutifs.

Multiplication, division, diviseurs

109 = 4 x 27 + 1 1/109 = 0,0091743119 2660550458 7155963302 7522935779 8165137614 6788990825 6880733944 9541284403 6697247706 4220183486 2385321100 917	Nombre premier en 4k + 1. Nombre premier de Chen. Nombre premier long Période 108; les derniers chiffres étant 8532 11, les nombres de Fibonacci à l'envers.
	Table de multiplication du nombre 109: saut d'une unité en plus ou en moins pour les unités, les dizaines et les centaines Principe valable pour de nombreux nombres en 111… – …11 comme 109

Avec les puissances

109 = (7^3 – 5^3) / 2 = (343 – 125) / 2	Deuxième nombre premier cubain d'ordre 2.
109 = 55² – 54²	Début d'une série de répétitions de chiffres en 111..1109.
109 = 3² + 10² = 3² + 6² + 8² = 1² + 2² + 2² + 10² = 1² + 6² + 6² + 6² = 2² + 4² + 5² + 8² = 1^3 + 3^3 + 3^3 + 3^3 + 3^3	Nombre binomial. Somme unique de deux carrés, car 109 est un premier en 4k + 1. Autres sommes de carrés et cubes. Voir aussi >>>
109 = 1^1 + 2^2 x 3^3	Premier de Pierpont: opération en 1, 2 et 3.
	Le produit de quatre nombres consécutifs plus 1 est un carré.

En puissance

= 2,555555397…	Racine présentant six décimales consécutives valant 5. Motif exceptionnel!
109² = 11 881 100² = 10 000 109² = 11 881 173² = 29 929 200² = 40 000 212² = 44 944 235² = 55 225 264² = 69 696 300² = 90 000	Plus petit carré avec trois 1. Plus petit nombre à trois chiffres, parmi cinq, dont le carré ne comporte que deux types de chiffres, hors centaines. 3 114² = 9 696 996 est le seul à quatre chiffres. 81 619² = 6 661 661 161, le seul à cinq chiffres et plus (semple-t-il). Hors nombres en 10…, 20… et 30…

Dénombrement, jeux et curiosités

Jeu du quatre 4. Avec la notation anglaise: .4 = 0, 4 = 2/5

Autour du nombre

Ce nombre est premier, sorte de Mersenne généralisé.

Décimales

109° 28’

Angle au centre du tétraèdre.

Nombre 109 et son inverse

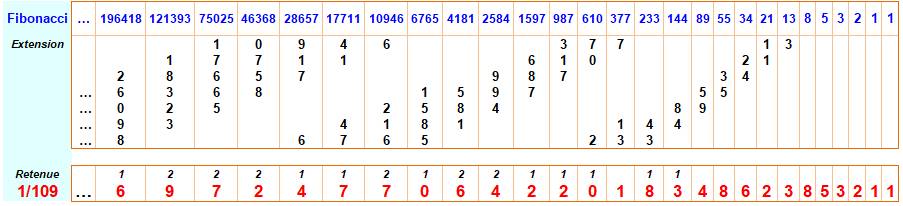
Nombre premier long. La période du développement décimal de la fraction est maximale (108). Toutes les fractions avec ce dénominateur présentent les mêmes chiffres permutés circulairement.

Étonnant ! Les décimales, de droite à gauche, sont le résultat de la sommation des nombres de Fibonacci successifs en tenant compte de la position des chiffres et des retenues. Illustration

Kaprekar découvrit que l'on retrouve toujours la période de 1/109 à une permutation près, en prenant deux nombres quelconques comme points de départ de la construction de Fibonacci. Il est vrai qu'avec les chiffres de la période de 1/109, pris deux à deux, on peut former toutes les combinaisons de deux chiffres de 0,0 à 9,9 en passant par 5,7 (exemple ci-dessous).

Construction de la période de 1/109 à partir des nombres de Fibonacci

Calcul des 27 dernières décimales de la période sur 108

Construction à partir de 5 et 7 et localisation de cet extrait dans la période de 1/109

0,0091743119266055045871559633027522935779816513761467889908

25688073394495412844036697247706422018348623853211

Voir Brève 659

Identité détaillée

Voir Diviseurs, Quantité, Somme, Fonctions arithmétiques

Numération: base, [chiffres]			Repdigit (Brésilien)
109 2, [1, 1, 0, 1, 1, 0, 1] 3, [1, 1, 0, 0, 1] 4, [1, 2, 3, 1] 5, [4, 1, 4] 6, [3, 0, 1] 7, [2, 1, 4] 8, [1, 5, 5] 9, [1, 3, 1] 10, [1, 0, 9] 11, [9, 10]	12, [9, 1] 13, [8, 5] 14, [7, 11] 15, [7, 4] 16, [6, 13] 17, [6, 7] 18, [6, 1] 19, [5, 14] 20, [5, 9] 21, [5, 4]	22, [4, 21] 23, [4, 17] 24, [4, 13] 25, [4, 9] 26, [4, 5] 27, [4, 1] 28, [3, 25] 29, [3, 22] 30, [3, 19] 60, [1, 49]	Aucun

Voir Bases / Brésiliens

Suite	Nombre 110 Autres nombres
Voir	Nombres par leur nom Empreinte des nombres DicoNombre Junior Historique de ce site et Références Maitres en nombres
Cette page	http://villemin.gerard.free.fr/NombDico/N100a500/Nb109.htm