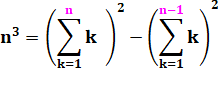|
Édition du: 30/04/2025 |
|
Dictionnaire des Nombres |
|||
|
1 / 10 / 50 / 70
/ 80 / 90
/ 100 / 105 / 106 / 107 / 108
/ 109 / 110 / 111 / 112
/ 113 / 114 / 115 / 116 / 117
/ 118 / 119 / 120 / 121 / 122
/ 123 / 124 |
125 |
126 / 127 / 128
/ 129 / 130 / 131 / 132 / 133
/ 134 / 135 / 140 / 150 / 160
/ 170 / 180 / 190 / 200 / 250
/ 300 / 400 / 500 / 1000
/ Autres |
|
![]()
|
|
|
|
|
Suite en propriétés
arithmétiques |
|
|
Chiffres et numération
|
125 =
25 x 5 |
|
|
125 +
521 = 646 |
|
|
125 = (1x1 + 2 + 2) x 5 x 5 |
|
|
1² + 2² + 5² =
1 + 4 + 25 |
|
Addition et soustraction
|
125 = 21 + 23 + 25 + 27 + 29 = 5 (1 + 3 + 5 + 7 + 9) = 5 + 15 + 25 + 35 + 45 |
Voir Brève
61-1213 |
|
|
125 =
8 + 9 + … + 17 |
|
|
Multiplication, division, diviseurs
|
Phi(125) =
100 |
|
|
Div(125) = {1, 5, 25,
125} 5 + 25 = 30 = 1² + 2² + 5² |
Nombre
canadien parfait. Ils sont quatre à partager cette propriété: 125, 581, 8
549 et 16 999. |
|
37, [125] 125 = 53 et 126 = 2x3²x7 => 42 – 5 = 37 |
Seul
nombre avec cette propriété jusqu'à au moins 109. |
Avec les puissances
|
125 =
53 512 = 83 |
Plus petit couple avec
des carrés: 12² = 144 et 21² = 441. |
|
125 =
2² + 11² = 5² + 10² |
|
|
|
|
|
125 =
53 = 15² – 10² = (10 + 5)² – 10² |
|
|
125 =
(1 + 2 + 3 + 4 + 5)² – (1 + 2 +
3 + 4 )² = 15² – 10² = 53 |
|
|
125 = 32 + 42 + 6² + 82 = 5² + 10² = 2² + 11² |
Voir Autour de 12345 |
|
125 =
5 (1 + 2) |
Nombre égal à une expression
utilisant ses propres chiffres. |
|
125 =
(1² + 2²) (3² + 4²) = (2² + 11²) = (5² + 10²) = 8² + 6² + 4² + 3² |
Voir
Brève 349 |
|
125 = 632 –
622 = 53 x 13 |
|
|
125 =
53 = 2² + 11² = 5² + 10² |
|
|
125 = 53 et 1 + 2
+ 5 = 8 = 23 125 = 53 et 1 =
1², 25 = 5² |
|
|
125 = 53 et 512 = 83 |
|
|
1253 =
1953125 |
||
|
125125 =
1299426220…9597369285104696… 0205078125 |
Liste: 125, 132, 147, 162, 163, 167,
169, 176, 186, 186, 188, 192, 197, … Voir 105 |
|
Dénombrement, jeux et curiosités
|
|
Avec
la notation anglaise: .4 = 0,4 = 2/5 |
Décimales
|
0,125
= 1 / 8 = 1 / 23 |
|
|
0,…125 =
2-(2k+1) |
|
![]()
|
|
Voir Diviseurs, Quantité, Somme, Fonctions arithmétiques
|
Numération: base, [chiffres] |
Repdigit (Brésilien) |
||
|
125 2,
[1, 1, 1, 1, 1, 0, 1] 3,
[1, 1, 1, 2, 2] 4, [1, 3, 3, 1] 5, [1, 0, 0, 0] 6,
[3, 2, 5] 7,
[2, 3, 6] 8,
[1, 7, 5] 9,
[1, 4, 8] 10,
[1, 2, 5] 11,
[1, 0, 4] |
12,
[10, 5] 13,
[9, 8] 14,
[8, 13] 15,
[8, 5] 16,
[7, 13] 17,
[7, 6] 18,
[6, 17] 19,
[6, 11] 20,
[6, 5] 21,
[5, 20] |
22,
[5, 15] 23,
[5, 10] 24, [5, 5] 25,
[5, 0] 26,
[4, 21] 27,
[4, 17] 28,
[4, 13] 29,
[4, 9] 30,
[4, 5] 60,
[2, 5] |
24,
[5, 5] 124,
[1, 1] |
Voir Bases / Brésiliens
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()