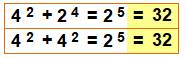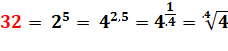|
Édition du: 05/03/2025 |
|
Dictionnaire des Nombres |
||||||||||||
|
100 / 200 |
||||||||||||
|
Maths générales du
32 |
Maths détaillées du 32 |
||
|
Géométrie avec 32 |
![]()
|
|
Nouvelle
orthographe avec
des traits d'union partout |
||
|
|
|||
|
Caractérisation
du nombre
|
|
Voir |
|
Rappel Propriétés générales >>>
![]()
Chiffres et numération
|
32
+ 23 = 55 = T10 |
|
|
|
323
= 32 768 32 =
(3x2) + (3+2+7+6+8) |
|
|
|
32
= 25 243
= 35 |
Les deux
seuls cas. |
|
|
32
= 100 000 en binaire |
||
|
1, 2, 3, …, 31, 32 =>
55 1, 2, 3, …, 220, 221 =>
555 |
|
|
|
32 =
34 – 2 = 4 x 23 = 43 / 2 |
|
|
Addition et soustraction
|
32
=
(8+1) + (8-1) + (8x1) + (8/1) = (6+3) +
(6-3) + (6x3) + (6/3) |
|
|
32 = 256 / 8 |
|
Multiplication, division, diviseurs
|
32
= 2 5 = 2 2 x 8 = 2 3 x 4 = 8 5/3 = (3 |
|
||||||||||
|
32 |
|
||||||||||
Période:
longueur du bloc qui se répète dans 1/p (ou 10n / p pour obtenir un
périodique pur) |
|||||||||||
|
32
= tau (840) |
|
|
31, [32, 36, 40, 45, 60,
1375] 32 = 25 et 33 = 3x11 => 33 – 2 = 31 |
|
Avec les puissances
Les
différentes manières d'exprimer 32 en puissances de 2

|
32²
= 1 024 = 210 |
|
|||
|
32 = 11 + 22
+ 33 |
|
|||
|
32 = 4² + 4²
= 1² + 2² + 3² + 3² + 3²
= 2² + 2² + 2² + 2² + 4²
= 23 + 23 + 23 + 23
= 24 + 24
= 25 |
|
|||
|
32 =
2 x 42 |
|
|||
|
32 =
24 + 42 |
|
|||
|
|
|
|||
|
32 = 26 –
25 |
|
|||
|
32
= 4 x 12 + 7
x 22 = 6 x 22 + 8
x 12 = 1 x 22 + 7
x 22 = 2 x 22 + 6
x 22 = 3 x 22 + 5
x 22 |
= 4 x 22 + 4
x 22 = 3 x 23 + 8 x
13 = 1 x 23 + 3
x 23 = 2 x 23 + 2
x 23 = 3 x 32 + 5
x 12 |
= 1 x 42 + 4
x 22 = 1 x 24 + 1
x 24 = 1 x 42 + 1
x 42 = 1 x 52 + 7
x 12 = 1 x 33 + 5
x 13 |
|
|
|
32
= (1 + i)8 + (1 – i)8 = (1 + i)9 + (1 – i)9 |
||||
|
32
et 324 = 1 048 576 |
|
|
323 = 32 768 |
|
|
324 = 1048576 494
= 5764801 864
= 54700816 |
|
Dénombrement, jeux et curiosités
|
|
|
|
24 faces 16 sommets |
|
SUITE
des propriétés du nombre 32 en
géométrie
Autour du nombre
|
32 |
Valeur de ce maximum à partir de 1 ×
1: |
|
|
32!
– 1 = 0,263130836… 1036 |
|
|
|
Pi = 3,1415926535
8979323846 2643383279 50… |
|
|
|
Écart 1,26
… 10-6 |
|
|
|
|
|
|
|
|
|
|
|
1 / 32,67 = 0,03 06 09 12 15 2 |
|
|
|
32,73373720…
|
|
|
|
32,72 72 72 …° = 360/11 |
|
|
|
|
Voir Diviseurs, Quantité,
Somme,
Fonctions
arithmétiques
|
Numération: base, [chiffres] |
Repdigit (Brésilien) |
||
|
2, [1, 0, 0, 0, 0, 0] 3,
[1, 0, 1, 2] 4, [2, 0, 0] 5,
[1, 1, 2] 6,
[5, 2] 7, [4, 4] 8, [4, 0] |
9,
[3, 5] 10,
[3, 2] 11,
[2, 10] 12,
[2, 8] 13,
[2, 6] 14,
[2, 4] |
15, [2, 2] 16, [2, 0] 17,
[1, 15] 18,
[1, 14] 19,
[1, 13] 20,
[1, 12] |
7,
[4, 4] 15,
[2, 2] 31,
[1, 1] |
Voir Bases
/ Brésiliens
![]()
|
Voir |
|
|
Site |
|
|
Cette
page |
![]()