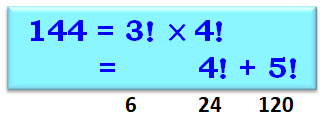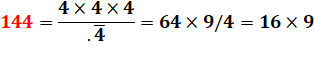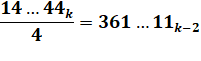|
Édition du: 22/03/2025 |
|
Dictionnaire des Nombres |
|||
|
1 / 10 / 50 / 70
/ 80 / 90
/ 100 / 110 / 120 / 125 / 126
/ 127 / 128 / 129 / 130 / 131
/ 132 / 133 / 134 / 135 / 136
/ 137 / 138 / 139
/ 140 / 141 / 142 / 143 |
144 |
145 / 146 / 147
/ 148 / 149 / 150 / 151 / 152
/ 153 / 154 / 155 / 160 / 165
/ 170 / 180 / 190 / 200 / 250
/ 300 / 400 / 500 / 1000
/ Autres |
|
![]()
|
Monsieur
de Lagny (1660-1734), de l'Académie des sciences se meurt et semble sans
connaissance. Monsieur de Maupertuis
(1698-1759), mathématicien et membre de la même Académie, promet à la famille
de le faire parler: – Quel est le carré
de douze? – Cent-quarante-quatre,
répondit le mourant et ce fut ses dernières paroles. D'après: Belles Histoires d'Humour de nos
ancêtres – Bernard Peyrous et Marie-Ange
Pompignoli Relaté aussi dans Point de Vue – Images
du Monde du 4 février 1972 |
Voir Pensées & humour
|
|
|
|||||||||||
Suite en propriétés
arithmétiques |
|
|
||||||||||
|
|
||
|
|
||
|
4 filles
et 4 garçons autour d'une table ronde: quantité de possibilités, en
préservant l'alternance. |
||
|
Accroche publicitaire de Cisco (juillet
2006). |
||
|
|
||
|
|
Chiffres et numération
|
144 = 12² 1 + 4 + 4 = 9 = 3² 1 × 4 × 4 = 16 = 4² 441 = 21² |
Voir Nombre
111 111 111 – Mêmes propriétés |
||
|
144 = (1×4×4) × (1+4+4) = 16 × 9 |
|
||
|
144 divisible par 9 et
16 |
|
||
|
144 / (1 + 4 + 4) = 16 144 / (1 × 4 × 4) = 9 |
|
||
|
|
|
||
|
144 + 441 = 585 144 × 441 = 63 504 = 2522 144 – 1×4×4 = 128 = 27 144 × 1×4×4 = 2 304 = 482 |
|
||
|
|
|
||
|
144 / (1 + 4 + 4) = 16 144
= (1 + 4 + 4) (1 x 4 x 4) 12²
= 3² × 4² |
|
|
144 = Sc { 33!, 34!
35!, 41! } |
|
Addition et soustraction
|
144 = 12 + 13 + … + 20
= 47 + 48 + 49 |
|
|
144 = T11 +
T12 = 66 + 78 = n² + 2n + 1 pour n = 11 |
|
|
144 = 71 + 73 |
|
|
144
= 71 + 73 144/2
– 1 = 71 |
Liste: 36, 144, 1764, 2304, 5184, 7056, 8100, 30276,
41616, 69696, 93636, 138384, 166464, … |
|
144 = 4! + 5! = 24 +
120 |
|
|
144 = 12² = 33 + 111 Notation: 12² = 31
+ 13 |
Au
début du Seigneur des anneaux, Frodon Bessac et Bilbon, son oncle, nés le
même jour, célèbrent respectivement leurs 33e et 111e
anniversaire, le 22 septembre T.A. 3001. |
|
144 = 1.2.3.4 +
2.3.4.5 = (2.3.4)(1+5) = 2.3.4.6 |
|
|
144 = 12² = 1 + 3 + 5
+ …+ 23 |
|
|
= 1 + 10 + 36 + 56 + 35 + 6 |
Il est
égal au carré de son rang: F12 = 144 = 12².
|
|
144 = 2 + 3 + 5 + … 13
+ 8 |
|
Multiplication, division, diviseurs
|
144 = 24 .
32 & 2 × 3 = 4 + 2 |
|
||
|
144 = 12 x 12
= 12² =
9 x 16 =
8 x 18 =
6 x 24 =
4 x 36 =
3 x 48 =
2 x 72 |
|
||
|
144 = (3 + 3 + 3 + 3)(3
+ 3 + 3 + 3) |
|
||
|
144 = 8 × 1 × 9 x 2
et 8 192 = 213 |
|
||
|
144 =
11 × 13 + 1 |
|
||
|
|
|
||
|
144 = 3! × 4! = 6 × 24
= 3! × 4 × 3! |
|
||
|
|
|
||
|
144 = 3! × 4! = 3! × (3! x 4)
=
3!² × 2² = 12² |
|
||
|
144 = 6! / 5 = 720 / 5
= 1 × 2 × 3 × 4 × 6 |
Voir Produit de
factorielles: 4! x 5! x 6! = 1440² |
||
|
144 = 10345
= 1! x 0! x 3! x 4! |
|
||
|
144 = 6 × 24
= (1 × 2 × 3) (1 × 2 × 3 × 4) |
|||
|
144 = 2 × 3 × 4 × 6 = (2×6) × (3×4) = 12² |
|
||
|
144 = tau (110 880) |
|
|
|
|
Avec les puissances
|
144 =
12² 12²
= 144
& 21² = 441 |
|
|
12² = 144 et
1 + 4 + 4 = 9 |
|
|
144 = 12² = 24
× 32 = 16
× 9
= 12 × 12 = 12²
= 24 × 6
= 10012 |
|
|
144 = 4² + 2 x 8²
= 6² + 3 x 6² = 4 × 6² |
|
|
144 = (6² + 6²) (1²+
1²)
= (12² + 0²)
= 6² + 6² + 6² + 6² |
|
|
144 = 20² – 16² = 12² =
6² x 2² |
|
|
144 = 12² et 1 + 4 + 4 = 9 = 3² 144 = 12² et 1 = 1², 4 = 2², 4 = 2² |
|
|
144
= 23 + 23 + 43 + 43 = 12² |
|
|
144 = 63 – 73 – 93 + 103
= 18 × 8 |
|
|
136²
+ 137² + … 144² =
145² + 146² … + 152² = 176 640 |
|
||
|
1445 =
275 + 845 + 1105 + 1335
= 61 917 3 64 224 |
|
||
|
1449 x 9 = 239 609 999 527 967 195 136 |
|
||
|
2144 = 2230
0745198530 6231415357
1827264836 1505980416 |
|
||
Dénombrement, jeux et curiosités
|
|
Avec
.4 surligné = 0,444… = 4/9. |
|
|
144 = 4! + 5! = 24 +
120 |
|
|
|
144 / 4 = 36
1444 / 4 = 361 14444 / 4 = 3611
…
|
|
||
|
1 444 = 38² |
|
||
|
|
|||
|
66, 70, 94, 115,
119 |
|
||
|
18 20 34 6 50 52 |
|
||
|
144 |
|
||
|
|
|||
|
–144 = ( |
|
||
|
144 × 441 = 252² |
|
||
|
10000/69
= 144,92 … 69
+ 39 + 36 = 144 |
Voir Nombre 198 |
||
|
|
Voir Diviseurs, Quantité, Somme, Fonctions arithmétiques
|
Numération: base, [chiffres] |
Repdigit (Brésilien) |
||
|
144 2,
[1, 0, 0, 1, 0, 0, 0, 0] 3,
[1, 2, 1, 0, 0] 4,
[2, 1, 0, 0] 5,
[1, 0, 3, 4] 6, [4, 0, 0] 7, [2, 6, 4] 8,
[2, 2, 0] 9,
[1, 7, 0] 10,
[1, 4, 4] 11, [1, 2, 1] |
12, [1, 0, 0] 13,
[11, 1] 14,
[10, 4] 15, [9, 9] 16,
[9, 0] 17, [8, 8] 18,
[8, 0] 19,
[7, 11] 20,
[7, 4] 21,
[6, 18] |
22,
[6, 12] 23, [6, 6] 24,
[6, 0] 25,
[5, 19] 26,
[5, 14] 27,
[5, 9] 28,
[5, 4] 29,
[4, 28] 30,
[4, 24] 60,
[2, 24 |
15,
[9, 9] 17,
[8, 8] 23,
[6, 6] 35,
[4, 4] 47,
[3, 3] 71,
[2, 2] 143,
[1, 1] |
Voir Bases / Brésiliens
![]()
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette
page |
![]()