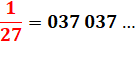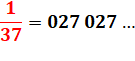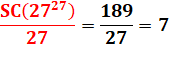Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 20/11/2024 M'écrire Brèves de Maths

DicoNombre Débutant Glossaire Types de nombres Nom des nombres Écriture des nombres Table des facteurs Langues	Dictionnaire des Nombres
	… / 0,001 / 0,1		0 à 99			100 / 200 / 300 / 400 / 500 / 600 / 700 / 800 / 900 / 1 000 / 2 000 / 5 000 / 10 000 / 100 000 / 10^6 / 10^9 / 10^100 / Infini
	-0-	10		20	30		40	50	60	70	80	90
	20	21		22	23		24	25	26	27	28	29

Nombre 27

Maths générales du 27

Maths détaillées du 27

Cycle avec 27

Vingt-sept

Twenty-seven

Nouvelle orthographe

avec des traits d'union partout

Facteurs
Binaire	1 1011
Bases	10003 1234 338
Romain	XX VII

Suite

Caractérisation du nombre

2/3-rond

Composé

Composé inévitable (ou minimal)

Déficient

Équidigital

Friable (3³)

Harshad

Hofstadter – NON

Impair

Narcissique de Keith

Narcissique généralisé

Puissant

Smith

Totient parfait

Van der Waerden

Cube

Décagonal (3^e)

Palindrome en binaire

Voir

Nom des nombres

Nombres selon langues

Nombres selon bases

Fonctions arithmétiques

Rappel Propriétés générales >>>

Chiffres et numération

			Motifs avec sommes et produits. Les trois seuls cas à deux chiffres. Voir Nombre 497
27 = 2+7 + 7+2+9	Narcissique de Keith Somme de ses chiffres et de ceux de son carré.
27 = (2 + 7) × 3	Seul nombre égal à trois fois la somme de ses chiffres.
27 = 3^3 = 338	Nombre faute de frappe en base 8.
2710 = 00 01 10 112	Amusement binaire: permutations à deux bits.
27 + 72 = 99 27 x 72 = 1 944 = 2^3 x 3^5 27 x (2 x 7) = 378 = T27 72 – 27 = 45 = T9		Devient repdigit en lui ajoutant son retourné et puissant avec le produit (le plus petit), etc. Table >>>
27 = (2+1) × (7+2)		Produit de ses chiffres augmentés régulièrement. Liste: 16, 27, 396, 117 729 612 000, …
27 => 2 + 7 = 9 3 x 3 x 3 => 3 + 3 + 3 = 9		Nombre de Smith.
27 = 3 x (2 + 7) 72 = 8 x (7 + 2)		Seul nombre trois fois somme de ses chiffres. 18 est le seul pour deux fois la somme. Son retourné est huit la somme.
27 = 16 038 / 594		Plus petite division pannumérique stricte.
27 = 1 + 9 + 6 + 8 + 3 et 1 9 6 8 3 = 27 ^3		Nombre égal à la somme des chiffres de son cube.

Addition et soustraction

p(27) = 3 010	Quantité de partitions du nombre.
26 = 3 + 23 = 7 + 19 = 13 + 13 27 = / 28 = 5 + 23 = 11 + 17	Plus petit nombre composé non somme de deux premiers. Liste: 27, 35, 51, 57, 65, 77, 87, 93, 95, 117, …
27 = 2 + 3 + 4 + 5 + 6 + 7 = 8 + 9 + 10 = 13 + 14		Seules sommes de nombres consécutifs >>>
15 = 1 + 2 + 3 + 4 + 5 27 = 1 + 2 + … + 4 + 7 429 = 4 + 5 + … + 29		Nombres étonnants: somme qui reprend ses chiffres pour les extrêmes. Voir Nombre 15 / Nombre 429
27 = 7 + 9 + 11 = 3 (1 + 3 + 5) = 3 (2 + 7)		Somme de trois impairs consécutifs. Seul nombre trois fois la somme de ses chiffres.
27 = 2 + 2 + 23 = 3 + 5 + 19 = 3 + 7 + 17 = 3 + 11 + 13 = 5 + 5 + 17 = 5 + 11 + 11 = 7 + 7 + 13			Plus petit nombre sept fois somme de trois nombres premiers.
27 = (6+2) + (6-2) + (6x2) + (6/2)		Somme des quatre opérations.

Multiplication, division, diviseurs

27 / (2 + 7) = 3	Le seul 3-Harshad.
27 = 3^3	Premier cube impair. Avec facteur cube.
	Curiosité due au fait que 27 × 37 = 999. Propriété que l'on retrouve pour les nombres en 10^n – 1.
Somme des diviseurs propres = 13	Le plus petit nombre déficient terminé par 7.
27 = 3^3 et 28 = 2^2.7	Les plus petits nombres successifs ayant trois facteurs avec les répétitions.

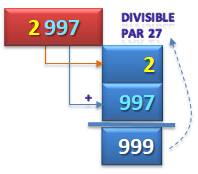
Clé de divisibilité par 27. Constituer des blocs de 3 chiffres et les additionner. Le résultat doit être divisible par 27. Avec cet exemple: 2 997 est divisible par 999 et par tous ses diviseurs: 1, 3, 9, 27, 37, 111, 333, 999 dont 27.

Il y a 9 nombres premiers inférieurs à 27 et, 27 est multiple de 9	Nombre MulQprem.
	Divisible par 27.
27 nombres	Tout entier est décomposable en somme d'au plus 27 nombres premiers.
	Nombre égal à trois fois la quantité de premiers qui lui sont inférieurs. Le plus petit cas. Liste des nombres : 27, 30, 33.
	Quantité de diviseurs de 900 Calcul: (2+1) (2+1) (2+1) = 27
	Deux antécédents aliquotes.

Avec les puissances

	Le seul cube qui diminué de 2 égal un carré (équation de Bachet). Voir Nombre 26 qui se trouve au milieu.
	Grands nombres avec des 3. Avec quatre 3 : 7 625 597 484 987. Avec cinq 3: 4,43426488… 10^38
27 – 2 = 25 = 5²	Le seul cube qui diminué de 2 égal un carré. Voir Nombre 26 qui se trouve au milieu.
27 = 1² + 1² + 5² = 3² + 3² + 3² = 1² + 1² + 3² + 4² = 1² + 2² + 2² + 3² + 3² = 3^3	Toutes les sommes de puissances de 2 à 5 avec deux à cinq termes.
27 = 4 x 3² – 3 x 3 = 1 + 9 + 17	3^e Nombre décagonal.
9 = 3² = 2^3 + 1 27 = 3^3 = 5^2 + 2	Seuls cas où carré et cube sont aussi proches. Voir Nombre 26
27 = 14² – 13² = 14 + 13 = 3^3 = 6² – 3² = (3 + 3)² – 3²	Motif général avec carrés. Motif général pour les cubes. Voir Autour de 12345
27 = 14^2 – 13^2 = 3^3 x 1^3	Différence de carré = produit de cubes.
27 = (1 + 2 + 3)² – (1 + 2)² = 6² – 3² = 3^3	Propriété
27 = 3 x 1^2 + 6 x 2^2 = 3 x 1^3 + 3 x 2^3 = 5 x 2^2 + 7 x 1^2 = 2 x 3^2 + 9 x 1^2 = 1 x 3^2 + 2 x 3^2 = 1 x 5^2 + 2 x 1^2	Autour des triplets de Pythagore. Carrés et autres puissances.
27 = 3.2^3 + 3.1^3 = 1.3^3	Exemple de l'égalité de Fermat.
27 = 1 + 2 + 8 + 16	Puissance de 3, somme de puissances de 2 distinctes.
27 = 6^3 – 5^3 – 4^3 = 3^3 = 19^3 – 18^3 – 10^3	Somme de trois cubes. Somme de cubes deux fois: 6^3 – 5^3 = 4^3 + 3^3
27 = 3^5 – 6^3 = 243 – 216	Différence entre puissances.
27 = 7 + 9 + 11	Cube = somme de nombres impairs consécutifs. Propriété générale des cubes.
27 = 1 + 12 + 14 = 2 + 9 + 16 = 4 + 6 + 17 341 = 1² + 12² + 14² = 2² + 9² + 16² = 4² + 6² + 17²		Égalités valables pour les entiers comme pour les carrés.

En puissance

27² = 729		Concaténation de deux premiers (7 et 29). Motif 27 et 72 Voir Calcul mental des carrés
27^3 = 19 683 27 = 1 + 9 + 6 + 8 + 3 = 3^3		Nombre NESCHIP. Le plus grand des cinq tels motifs. 19 6383 est un nombre doublement cube
27^4 = 531 441		Bicarré avec chiffres jusqu'à 4.
18^4 = 104 976 & 1+0+4+9+7+6 = 27 27^4 = 531 441 & 5+3+1+4+4+1 = 18			Motif en couple.
27^7 = 10 460 353 203 & 1+0+4+…+0+3 = 27			Nombre NESCHIP.
	Somme des chiffres n^n divisible par n. Liste: 1, 2, 3, 9, 18, 27, 54, 90, 108, 163, 197, 254, 432, 1292, 2202, 9648, … OEIS A108827
2^27 = 1342 17 728 => 13 177 premier	La suite des chiffres impairs forme un nombre premier. Plus petit à cinq chiffres.

Dénombrement, jeux et curiosités

	Jeu du quatre 4.
27, 111, 78, 9 232, 95	Le cycle de Syracuse converge toujours vers 1 en un nombre d'itérations plus ou moins important. Avec 27, il atteint un record en donnant les trois valeurs suivantes: Durée de vol: 111 Altitude: 9 232 au rang 78 Durée en altitude: 95

Le cycle de Syracuse pour n = 27

27, 82, 41, 124, 62, 31, 94, 47, 142, 71, 214, 107, 322, 161, 484, 242, 121, 364, 182, 91, 274, 137, 412, 206, 103, 310, 155, 466, 233, 700, 350, 175, 526, 263, 790, 395, 1186, 593, 1780, 890, 445, 1336, 668, 334, 167, 502, 251, 754, 377, 1132, 566, 283, 850, 425, 1276, 638, 319, 958, 479, 1438, 719, 2158, 1079, 3238, 1619, 4858, 2429, 7288, 3644, 1822, 911, 2734, 1367, 4102, 2051, 6154, 3077, 9232, 4616, 2308, 1154, 577, 1732, 866, 433, 1300, 650, 325, 976, 488, 244, 122, 61, 184, 92, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1

Autour du nombre

27 x 37 = 999 123 / (27 x 37) = 0,123123123…		Produit engendrant de nombreuses propriétés.
1/27 = 0, 037 037 037... 1/37 = 0, 027 027 027...		Plus petit nombre périodique de période égale à 3. Motifs échangés amusants.
27 & 37 27 x 9 = 189 et 891 = 33 x 27		Deux seuls nombres ayant la propriété suivante: on considère leurs multiples à trois chiffres. Leurs permutations cycliques restent des multiples.
27! + 1	Générateur de nombres premiers factoriels. Factorielle plus 1 donne un nombre premier.

Suite infinie de carrés avec des nombres en 266…667 Avec k "6", le carré contient k fois le "1" et k fois le "8". V. Thébault- 1943 Ces sortes de suites sont très nombreuses Exemple de multiplication posée =>

Identité détaillée

Voir Diviseurs, Quantité, Somme, Fonctions arithmétiques

Numération: base, [chiffres]			Repdigit (Brésilien)
2, [1, 1, 0, 1, 1] 3, [1, 0, 0, 0] 4, [1, 2, 3] 5, [1, 0, 2] 6, [4, 3] 7, [3, 6] 8, [3, 3]	9, [3, 0] 10, [2, 7] 11, [2, 5] 12, [2, 3] 13, [2, 1] 14, [1, 13]	15, [1, 12] 16, [1, 11] 17, [1, 10] 18, [1, 9] 19, [1, 8] 20, [1, 7]	8, [3, 3] 26, [1, 1]

Voir Bases / Brésiliens

Suite	Voir le menu en haut de page
Cette page	http://villemin.gerard.free.fr/NombDico/Nb27Nb.htm