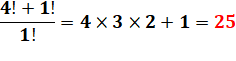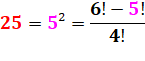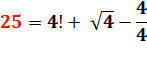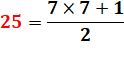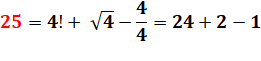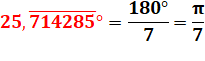Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 18/01/2024 M'écrire Brèves de Maths

DicoNombre Débutant Glossaire Types de nombres Nom des nombres Écriture des nombres Table des facteurs Langues	Dictionnaire des Nombres
	… / 0,001 / 0,1		0 à 99			100 / 200 / 300 / 400 / 500 / 600 / 700 / 800 / 900 / 1 000 / 2 000 / 5 000 / 10 000 / 100 000 / 10^6 / 10^9 / 10^100 / Infini
	-0-	10		20	30		40	50	60	70	80	90
	20	21		22	23		24	25	26	27	28	29

Nombre 25

Maths générales du 25

Maths détaillées du 25

Vingt-cinq

Twenty-five

Nouvelle orthographe

avec des traits d'union partout

Facteurs
Binaire	1 1001
Bases	1214
Romain	XX V

Suite

Humour

31₈ = 25₁₀

31 en octal = 25 en décimal

Autre écriture avec OCT pour octal et DEC pour décimal:

31 OCT = 25 DEC

Autrement dit: Halloween et Noël sont équivalents!

Caractérisation du nombre

2-rond

Aspirant

Automorphe

Binomial

Brillant

Carré

Chanceux

Composé

Composé inévitable (ou minimal)

Coster

Cullen (3٠2³ +1)

Déficient

Dihédral

Docile (amenable)

Friedman (5²)

Glissant

Idonéal

Impair

Narcissique de Keith

Proth

Puissant

Ramsey (4,5) et (7,7,7)

Ruth-Aaron avec 24

Semi-premier

Stirling 1^ère espèce

Trimorphe

Carré (5^e)

Carré centré (4^e)

Octogonal centré (3^e)

Octaédrique centré (3^e)

Voir

Nom des nombres

Nombres selon langues

Nombres selon bases

Fonctions arithmétiques

Rappel Propriétés générales >>>

Propriétés MATHÉMATIQUES

Voir Pépites / Triplet le plus célèbre

Chiffres et numération

25	N'est repdigit dans aucune base. Il n'est pas brésilien.
2 × 5 = 10 => 1 ×0 = 0		Persistance multiplicative égal à 2 (deux itérations).
25 = 5²		Anagrammes numériques. Nombre de Friedman.
25 = 3+9+0+6+2+5 25^4 = 390 625		Narcissique de Keith Somme des chiffres de sa puissance 4.
25 et 36		Deux carrés à chiffres incrémentés
25 = 5 x 5		Nombre égal à cinq fois ses unités.
25 = (2 + 2) 5 + 5		Nombre de Coster (opérations utilisant deux fois ses chiffres). Motif valable pour tous les nombres à deux chiffres terminés par 5.
25 = 1 + 2 x 3 x 4		Motif avec nombres consécutifs.
25 + 52 = 77 52 – 25 = 27 = 3^3		Devient repdigit lorsqu'ajouté à son retourné et cube en retranchant.

Addition et soustraction

p(25) = 1 958	Quantité de partitions du nombre.
25 = 3 + 4 + 5 + 6 + 7 = 12 + 13	Seules sommes de nombres consécutifs >>>
25 = T4 + T5 = 10 + 15	Somme de nombres triangulaires consécutifs.
25 = 5² = 1 + 4 + 8 + 12 = 1 + 2 x 3 x 4 = 5² = 1 + 3 x 8		5^e Nombre carré. Nombre carré centré n° 4. Seul carré et carré centré. Plus petit nombre trois fois polygonal. Tous les carrés des nombres impairs sont en 1 + 8k.
25 = 5² = 3 + 4 + 5 + 6 + 7		Somme d'entiers consécutifs = carré.
25 = 1 + 3 + 5 + 7 + 9 = (1 + 9)² / 4 = 100 / 4		Somme de 5 impairs consécutifs. Propriété de tous les carrés: la somme des impairs jusqu'à n est égale à la demi-somme des extrêmes au carré: (1 + n)² / 4.
25 = 2 + 23 = 3 + 5 + 17 = 5 + 7 + 13 = 2 + 3 + 7 + 13 = 2 + 5 + 7 + 11 = 2 + 3 + 5 + 7 + 8		Plus petit nombre somme de deux, trois, quatre et cinq nombres premiers. Voir Exemple de telles partitions en 43.
25 + 26 + 27 + 28 + 29 + 30 = 31 + 32 + 33 + 34 + 35		Somme de nombres consécutifs. Propriété de tous les carrés.
25 = (4+4) + (4-4) + (4x4) + (4/4)		Somme des quatre opérations.
			Nombre glissant.

Multiplication, division, diviseurs

Opérations: c'est facile avec le nombre 25, le quart de 100

25 x 25 = 625	Le produit de deux nombres se terminant par 25 se termine lui-même par 25. Seul autre cas: 76. Et ça continue avec 625 et 376.
25 = 4! + 1	Factorielle carrée. Voir problème de Brocard en 4
		Division avec des factorielles.

25 = 12 x 2 +1 25 = 8 x 3 + 1 25 = 6 x 4 + 1 25 = 5 x 5		Nombre avec restes 1 lorsque divisé par les nombres de 2 à 4 et divisible par le suivant 5.
25 => 2 x 5 = 10 => 1 x 0 = 0		Plus petit nombre de persistance multiplicative égale à 2.
		Carré = cette relation entre factorielles successives.
				Trois antécédents aliquotes.
= 1+1+2+2+4+2+…+22+8+20 = 1000			Sommes des totients des nombres de 1 à 25.
21, [25, 2 299, 18 490] 25 = 5² et 26 = 2x13 => 26 – 5 = 23			Plus petit nombre tel que son radical est égal au radical du suivant moins k donné.
	Suite aliquote aboutissant à un nombre parfait. Liste pour 6 en fin: 6, 25, 95, 119, 143 Aucun se terminant par 28, sauf 28.

Avec les puissances

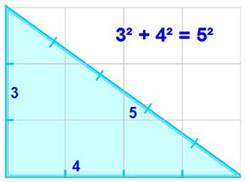
25 = 3² + 4² = 5²	Premier et plus beau Triplet de Pythagore. Triangle sacré Somme des carrés de nombres consécutifs. Suivant: 841. Nombre binomial.
25 = 0² + 5² = 3² + 4²	Somme de puissances. Deux fois somme de 2 carrés.
25 = 13² – 12² = 13 + 12 = 5²	Différence de deux carrés. Triplets de Pythagore. Motif général.
25 = 13² – 12² = 5² = 5² x 1²	Nombre complètement carré.
25 = (1² + 2²) (1² + 2²) = (3² + 4²) = (5² + 0²) = 3² + 3² + 1² + 1²	Somme de carrés, produit de somme de carrés. Nombre de Brahmagupta. Seul nombre impair (> 1) non somme de trois carrés
25 = 3 x 2^3 + 1 = 1^3 + 2^3 + 2^3 + 2^3	Nombre de Cullen. Carré, somme de quatre cubes.
25 = 1 + 6 + 18 = 5² et 1² + 6² + 18² = 19² = 361 25 = 1 + 12 + 12 = 5² et 1² + 12² + 12² = 17² = 289	Somme carrée dont la somme des carrés des termes est aussi un carré. Double motif.

	Carré égal moyenne de carrés.
25 = 1 x 1^2 + 6 x 2^2 = 5 x 1^2 + 5 x 2^2 = 1 x 1^3 + 3 x 2^3 = 4 x 2^2 + 9 x 1^2 = 2 x 2^3 + 9 x 1^3 = 2 x 3^2 + 7 x 1^2 = 1 x 3^2 + 4 x 2^2 = 1 x 2^4 + 9 x 1^4 = 1 x 4^2 + 9 x 1^2 = 1 x 4^2 + 1 x 3^2	Autour des triplets de Pythagore. Carrés et autres puissances.
	Le seul carré qui augmenté de 2 égal un cube (équation de Bachet). Voir Nombre 26 qui se trouve au milieu.
25 = 5^3 – 10^2	Différence entre puissances. Seul cas d'équation de Bachet pour k = 25. Différence entre un cube et un carré.
25 = 5²	Le plus petit nombre de Friedman: nombre calculé avec ses propres chiffres. Le suivant est 121.
25 = (7 – 2) ^(7 – 5)	Curiosité avec les chiffres de 25 complémentés à 7.
	Curiosité avec la racine quatrième.
	Jeu du quatre 4 avec quatre"4". Et aussi avec seulement deux "4" Avec la notation: .racine(4) = 0,2 = 1/5

En puissance

625 = 25²	Nombre plaqué carré ou automorphique. Seul nombre à deux chiffres avec 76 qui, en ajoutant un nombre à gauche, donne son carré (376 et 625 pour trois chiffres).
25 = 5² 27 = 25 + 2 = 3^3	Seuls carré et cube distant de 2.
2^25 = 33 554 432	Dernière puissance de 2 sans les chiffres 7, 8 et 9. Au-delà, elles comportent au moins un 7 ou un 8 ou un 9. Notez le motif répétitif des chiffres.
25² = 7² + 24² = 49 + 576 = 625 = 15² + 20² = 225 + 400	4^e triplet de Pythagore primitif. 3^e avec hypoténuse = côté – 1. Plus petit nombre somme de deux carrés deux fois.
24² = 25² – 50 + 1 = 576 26² = 25² + 50 + 1 = 676	Calcul mental des carrés à partir de 25². Écart de 100 et, donc, chiffres semblables.
25^3 = 15625	Nombre plaqué cube.

Propriété des trois derniers chiffres des puissances de 25

Une puissance de 25 (>1)se termine toujours par 625

Voir Cas de 51 / Cas de 55 / Cas général des nombres en 5

25^3 = 75² + 100² = 44² + 117² = 35² + 120²	Cube somme de deux carrés.
25^3 = 4^3 + 17^3 + 22^3 = 1^3 + 2^3 + 4^3 + 12^3 + 24^3	Cube somme de trois cubes distincts. Pas somme de 2 ou 4 cubes distincts. Dix fois somme de cinq cubes distincts.
25^4 = 390 625 & 3+9+0+6+2+5 = 25	Nombre NESCHIP: somme des chiffres de sa puissance quatrième.
25^5 = 9765625 => 9+7+6+…+5 = 40 40^8 = 6553600000000 => 6+5+5+…+0 = 25 40^11 = 419430400000000000 => 4+1+9+…+0 = 25		Motif en couple.
…25^k = ….25	Tous les nombres terminés en 25, élevés à une puissance quelconque se terminent par 25. C'est le seul cas avec 76. Voir Puissances de 10

Dénombrement, jeux et curiosités

25 cases noires et 24 blanches (ou l'inverse) sur une grille 7×7. Quantité de cases comme celle du coin: n² / 2 si n est pair; et (n² + 1) / 2 si n est impair.

			Jeu du quatre 4.
{2, 3, 5, 7, 11 … 83, 89, 97}			Il y a 25 nombres premiers jusqu'à 100. Voir la barre magique des nombres premiers ou comment trouver et mémoriser facilement ces 25 nombres.
25, 23, 7, 88 Cycle: 25, 76, 38, 19, 58, 29, 88, 44, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1		Le cycle de Syracuse de 25 comporte 23 étapes, un record. Il atteint une altitude maximale avec 88 au rang 7.
25 = 5 / 0,2		Forme peu familière, objet de question dans les jeux.
25 = 8 x 3 + 1		Nombre octogonal centré.
25	Nombre chanceux d'Ulam.
25	Pavages du plan avec des polygones tels que les sommets sont équivalents; dont onze convexes.

Autour du nombre

25 x 10^4 = 1 + 3 + 5 + … + 997 + 999 = (1 + 999)² / 4	La somme des impairs jusqu'à n est égale à la demi-somme des extrêmes au carré: (1 + n)² / 4.
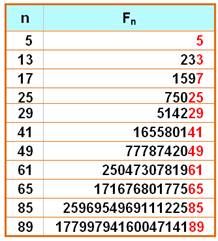
F25 = 75 025 = 5² x 3 001	25^e nombres de Fibonacci. Le plus grand à cinq chiffres. Le plus petit étant: 10 946

Décimales

= 25,714285 714285 7 …	Angle de l'heptagone étoilé régulier.
25,80645161 =	Nombre faute de frappe
	La racine du mal ! Voir Nombre de la Bête
25,980…	Multiple proche d'un entier.

Identité détaillée

Voir Diviseurs, Quantité, Somme, Fonctions arithmétiques

Numération: base, [chiffres]			Repdigit (Brésilien)
2, [1, 1, 0, 0, 1] 3, [2, 2, 1] 4, [1, 2, 1] 5, [1, 0, 0] 6, [4, 1] 7, [3, 4] 8, [3, 1]	9, [2, 7] 10, [2, 5] 11, [2, 3] 12, [2, 1] 13, [1, 12] 14, [1, 11]	15, [1, 10] 16, [1, 9] 17, [1, 8] 18, [1, 7] 19, [1, 6] 20, [1, 5]	24, [1, 1]

Voir Bases / Brésiliens

Suite	Voir le menu en haut de page
Cette page	http://villemin.gerard.free.fr/NombDico/Nb25Nb